Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
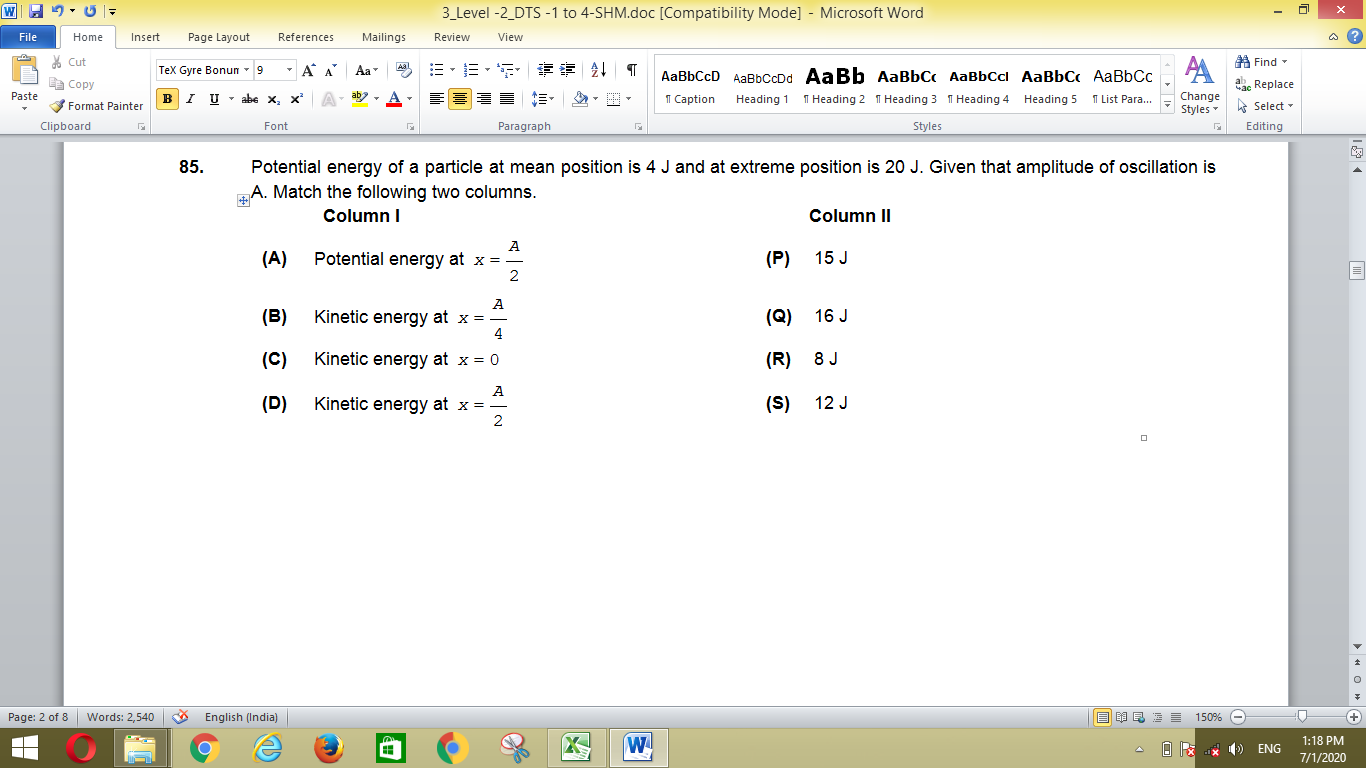
- Potential energy of a particle at mean position is 4 J and at extreme ...
Text Solution
|
- A linear harmonic oscillator has a total mechanical energy of 200 J . ...
Text Solution
|
- The total energy of a particle executing S.H.M. is 80 J . What is the ...
Text Solution
|
- In position A kinetic energy of a particle is 60 J and potential energ...
Text Solution
|
- The total energy of a harmonic oscillator of mass 2 kg is 9 J. If its ...
Text Solution
|
- The potential energy of a partical is SHM is 2 xx 10^(-4) J at the ext...
Text Solution
|
- A particle executing S.H.M. has total energy of 20 J. If the potential...
Text Solution
|
- A particle executing S.H.M. has total energy of 20 J. If the potential...
Text Solution
|
- The potential energies of a linear harmonic oscillator at the mean pos...
Text Solution
|