A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
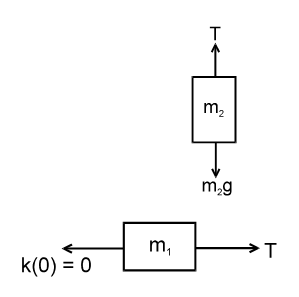
- m1 & m2 are connected with a light inextensible string with m1 lying...
Text Solution
|
- Three blocks of masses m1, m2 and m3 are connected as shown in the fig...
Text Solution
|
- A light string passing over a smooth light pulley connects two blocks ...
Text Solution
|
- Two blocks of masses m1 and m2, which are connected with a light strin...
Text Solution
|
- m1 & m2 are connected with a light inextensible string with m1 lying...
Text Solution
|
- A light string passing over a smooth light pulley connects two blocks ...
Text Solution
|
- If m1 = 10 kg, m2 = 4kg and m3=2kg the tension in the string connecti...
Text Solution
|
- A lift can move upward (or) downward. A light inextensible string fixe...
Text Solution
|
- Three blocks of masses m1, m2 and m3 are connected as shown in the fig...
Text Solution
|