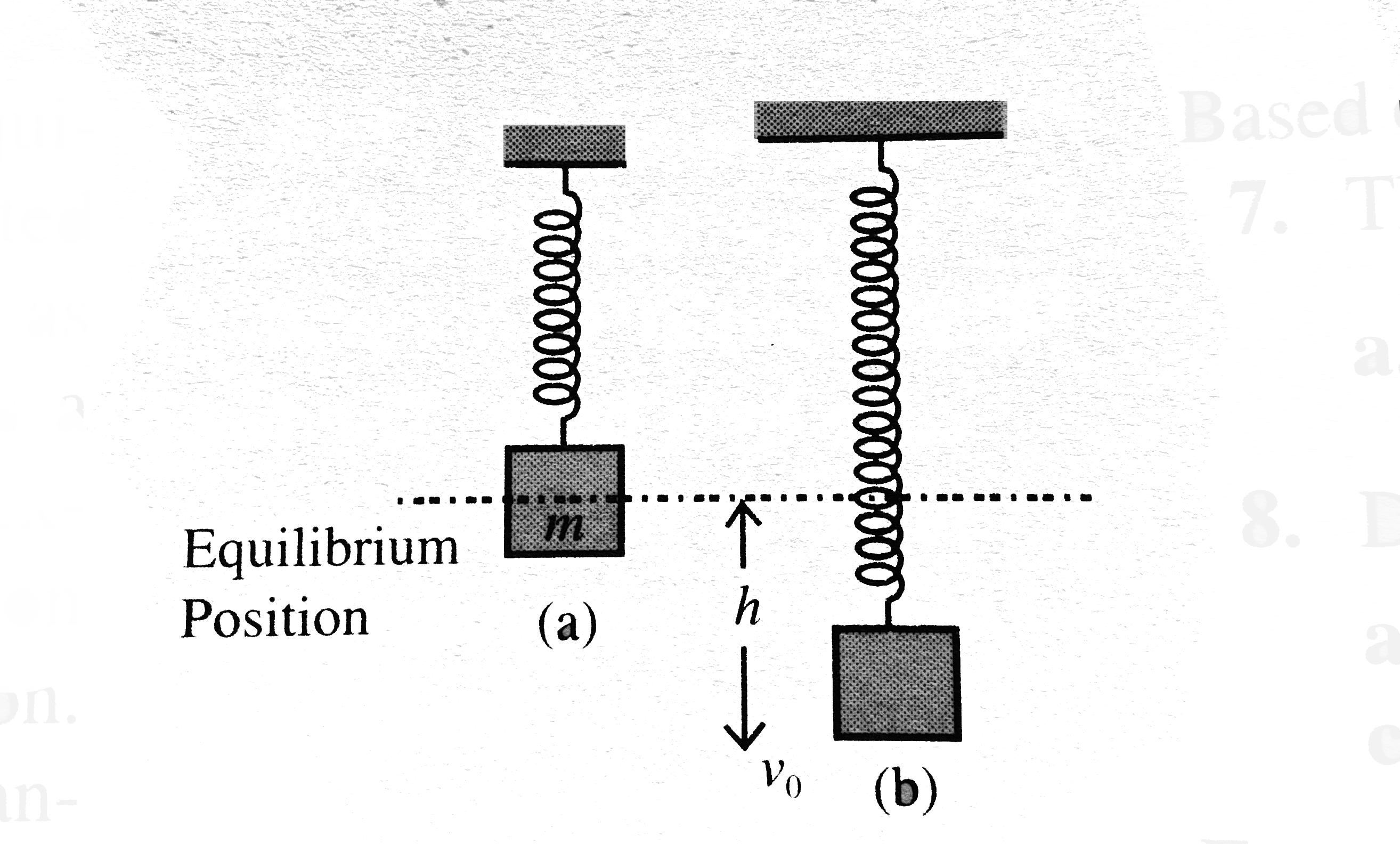A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- A block of mass m is connected to a spring constant k and is at rest i...
Text Solution
|
- A block of mass m is connected to a spring constant k and is at rest i...
Text Solution
|
- A block of mass m is connected to a spring constant k and is at rest i...
Text Solution
|
- A block of mass m is connected to a spring constant k and is at rest i...
Text Solution
|
- A block of mass m is connected to a spring of spring constant k as sho...
Text Solution
|
- A 100 g block is connected to a horizontal massless spring of force co...
Text Solution
|
- A 100 g block is connected to a horizontal massless spring of force co...
Text Solution
|
- A 100 g block is connected to a horizontal massless spring of force co...
Text Solution
|
- A 100 g block is connected to a horizontal massless spring of force co...
Text Solution
|