Home
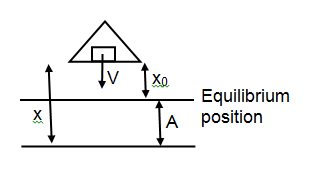
Class 12
PHYSICS
A body of mass m is released from a heig...

A body of mass `m` is released from a height h to a scale pan hung from a spring. The spring constant of the spring is `k`, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is

A

`mg/k`

B

`mg/ksqrt((1+(2hk)/mg))`

C

`mg/k+mg/ksqrt((1+(2hk)/mg))`

D

`mg/ksqrt((1+2hk)/(mg) (mg)/k))`

Text Solution

Verified by Experts

The correct Answer is:
B
Let x be the maximum elongation of spring. From conservation of energy,
`(1)/(2)kx^(2)=mgx+(1)/(2)mV^(2)` And `V=sqrt(2gh)`
Solving `x=(mg)/(k)+(mg)/(k)sqrt(1+(2hk)/(mg))`
Let `x_(0)` be the elongation in equilibrium position, then `x_(0)=(mg)/(k)`
So `A=x-x_(0)=(mg)/(k)+(mg)/(k)sqrt(1+(2hk)/(mg))`
Promotional Banner

Similar Questions

Explore conceptually related problems

A load of mass m falls from a height h on to the scale pan hung from a spring , as shown in the figure . If the spring constant is k , mass of the not bounce , relative to the pan , then the amplitude of vibration is

A block is released from height h , find the maximum compression of spring of spring constant k .

A block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is

A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x then

A body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is

A body of mass m falls from a height h on to the pan of a spring balance. The masses of the pan and spring are negligible. The spring constant of the spring is k. Having stuck to the pan the body starts performing harmonic oscillations in the vertical direction. Find the amplitude and energy of oscillation.

A solid ball of mass m is made to fail from a height H on a pan suspended through a spring of spring constant K as shown in figure. If the does not rebound and the pan is massless, then amplitude of oscillation is