Home
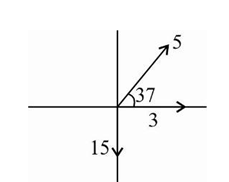
Class 12
PHYSICS
The resultant amplitude due to superposi...

The resultant amplitude due to superposition of three simple harmonic motions `x_(1) = 3sin omega t`,
`x_(2) = 5sin (omega t + 37^(@))` and `x_(3) = - 15cos omega t` is

A

18

B

10

C

12

D

none of

Text Solution

Verified by Experts

The correct Answer is:
D
`x_(1)=3sinomegat`
`x_(2)=5sin(omegat+37^(@))`
`x_(3)=15sin(omegat+pi+(pi)/(2))`
`A_(R)=sqrt(A_(x)^(2)+A_(y)^(2))=sqrt((7)^(2)+(12)^(2))=sqrt(49+144)=sqrt(193)`
Promotional Banner

Similar Questions

Explore conceptually related problems

Find the resultant amplitude of the following simple harmonic equations : x_(1) = 5sin omega t x_(2) = 5 sin (omega t + 53^(@)) x_(3) = - 10 cos omega t

The resultant amplitude due to super position of x_(1)=sin omegat, x_(2)=5 sin (omega t +37^(@)) and x_(3)=-15 cos omega t is :

x_(1) = 3 sin omega t x_(2) = 5 sin (omega t + 53^(@)) x_(3) = - 10 cos omega t Find amplitude of resultant SHM.

If i_(1) = 3 sin omega t and i_(2) =6 cos omega t , then i_(3) is

Find the displacement equation of the simple harmonic motion obtained by combining the motion. x_(1) = 2sin omega t , x_(2) = 4sin (omega t + (pi)/(6)) and x_(3) = 6sin (omega t + (pi)/(3))

The ratio of amplitudes of following SHM is x_(1) = A sin omega t and x_(2) = A sin omega t + A cos omega t

The epoch of a simple harmonic motion represented by x = sqrt(3)sin omegat + cos omega t m is

If i_(1)=3 sin omega t and (i_2) = 4 cos omega t, then (i_3) is