A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
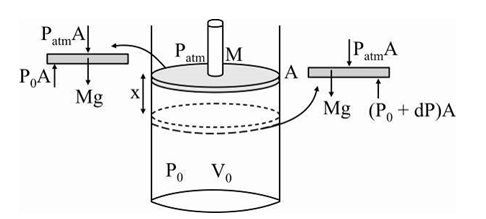
- An ideal gas enclosed in a vertical cylindrical container supports a f...
Text Solution
|
- An ideal gas enclosed in a cylindrical container supports a freely mov...
Text Solution
|
- An ideal gas enclosed in a cylindrical container supports a freely mov...
Text Solution
|
- A closed and isolated cylinder contains ideal gas. An adiabatic separa...
Text Solution
|
- एक आदर्श गैस ऊध्वार्धर बेलनाकार बर्तन में भरी है जो M द्रव्यमान की मुक...
Text Solution
|
- A piston of cross-section area A is fitted in a cylinder in which gas ...
Text Solution
|
- एक ऊर्ध्वाधर बेलनाकार बर्तन में भरी आदर्श गैस स्वतंत्रतापूर्वक चलायमान...
Text Solution
|
- An ideal gas is enclosed in a vertical cylindrical container and suppo...
Text Solution
|
- An ideal gas enclosed in a vertical cylindrical container supports a f...
Text Solution
|