Home
Class 12
PHYSICS
The x-t graph of a particle undergoing s...

The `x-t` graph of a particle undergoing simple harmonic motion is shown below. The accelertion of the particle at `t = 4//3 s` is

A

`(sqrt3)/(32)pi^(2)cm//s^(2)`

B

`(-pi^(2))/(32)pi^(2)cm//s^(2)`

C

`(pi^(2))/(32)pi^(2)cm//s^(2)`

D

`-(sqrt3)/(32)pi^(2)cm//s^(2)`

Text Solution

Verified by Experts

The correct Answer is:
D
The given motion is represented by
`(omega=(2pi)/(T)=(2pi)/(8)=(pi)/(4))`
`x=1sin((pi)/(4)t)`,`(d^(2)x)/(dt^(2))=(-pi^(2))/(16)sin (pi//4)t`
At `t=4//3s`,`(d^(2)x)/(dt^(2))=-(sqrt3)/(32)pi^(2)cm//s^(2)`
Promotional Banner

Similar Questions

Explore conceptually related problems

The x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at t = 2/3s is

The x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle of t=4//3s is

The x-t graph of a particle undergoing simple harmonic motion is shown in figure. Acceleration of particle at t = 4//3 s is

The total energy of a particle executing simple harmonic motion is

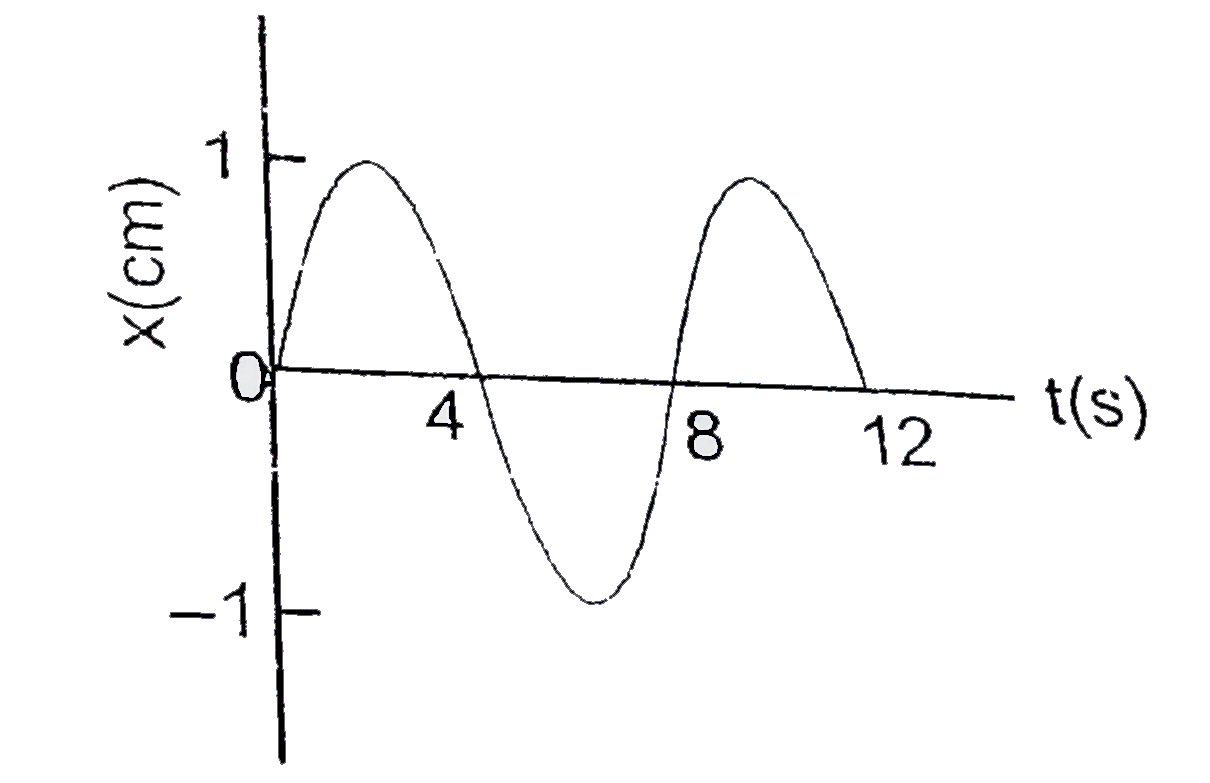
The x-t graph of a particle undergoing SHM is as shown in figure. The acceleration of the particle at t=2//3 is

The displacement vs time graph of a particle undergoing S.H>M. Is shown below . The acceleration of the particle at t=2//3s is

The velocity of a particle executing simple harmonic motion is

While a particle executes linear simple harmonic motion

The phase (at a time t) of a particle in simple harmonic motion tells

If a particle is executing simple harmonic motion, then acceleration of particle