A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
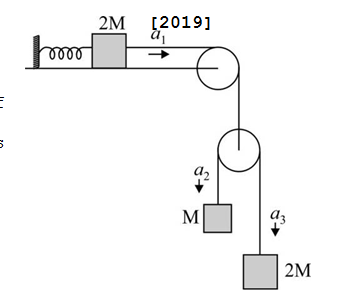
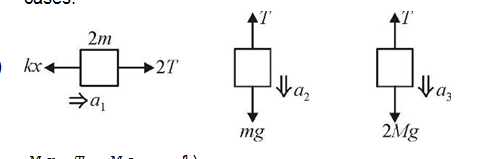
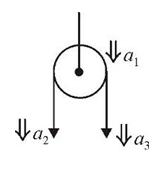
- A block of mass 2M is attached to a massless spring with spring-consta...
Text Solution
|
- A block of mass m is connect to another block of mass M by a massless ...
Text Solution
|
- A block of mass m is connected to another block of mass M by a massles...
Text Solution
|
- The given arrangement is released from rest when spring is in natural ...
Text Solution
|
- Two springs are in a series combination and are attached to a block of...
Text Solution
|
- A block of mass m is connected to another .block of mass M by a massle...
Text Solution
|
- Blocks A and B shown in the figure are having equal masses m. The syst...
Text Solution
|
- A block of mass 2M is attached to a massless spring with spring-consta...
Text Solution
|
- 2M द्रव्यमान का एक गुटका एक भारहीन स्प्रिंग , जिसका स्प्रिंग नियतांक k...
Text Solution
|