A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
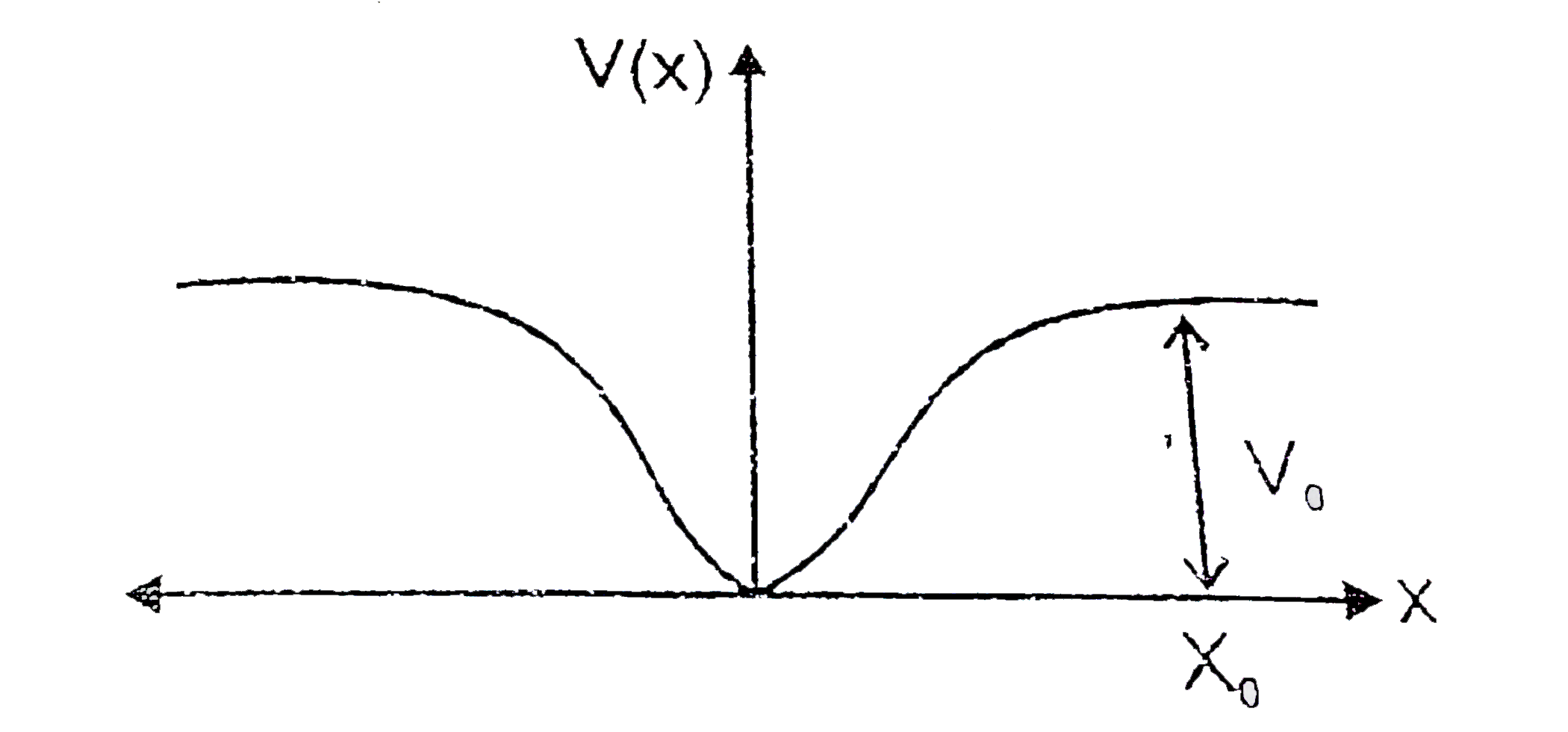
- When a particle is mass m moves on the x- axis in a potential of the f...
Text Solution
|
- A particle of mass 2 kg moves in simple harmonic motion and its potent...
Text Solution
|
- The potential energy of a particle with displacement X is U(X). The mo...
Text Solution
|
- When a particle is mass m moves on the x- axis in a potential of the f...
Text Solution
|
- जब m द्रव्यमान का एक कण :-अक्ष पर V(x) = kx^(2)', स्थितिज ऊर्जा से गति...
Text Solution
|
- जब m द्रव्यमान का एक कण :-अक्ष पर V(x) = kx^(2)', स्थितिज ऊर्जा से गति...
Text Solution
|
- जब m द्रव्यमान का एक कण :-अक्ष पर V(x) = kx^(2)', स्थितिज ऊर्जा से गति...
Text Solution
|
- जब m द्रव्यमान का एक कण X -अक्ष पर V (x )=kx ^(2 ) स्थितिज ऊर्जा से गत...
Text Solution
|
- A particle of mass m is executing oscillations about the origin on the...
Text Solution
|