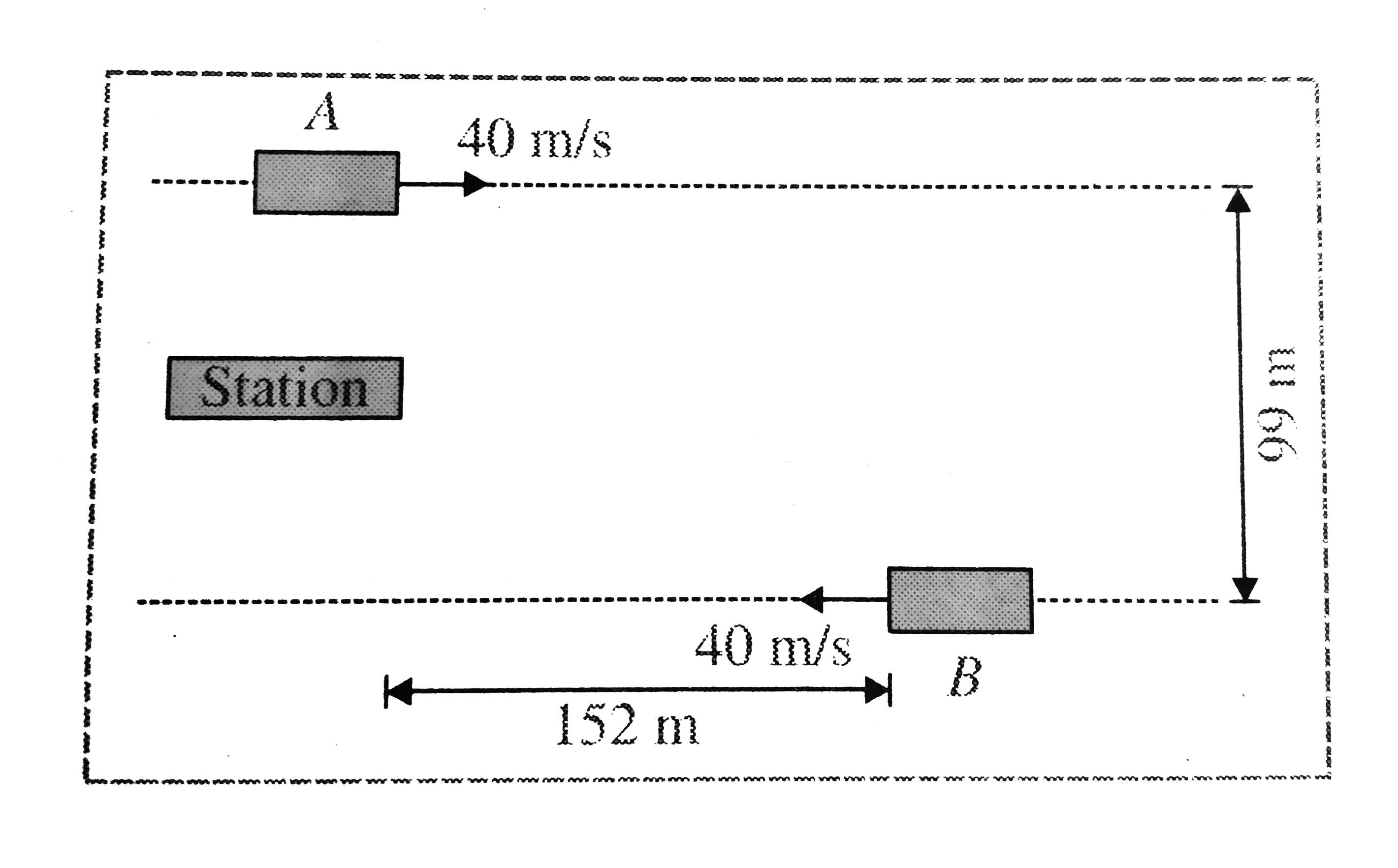
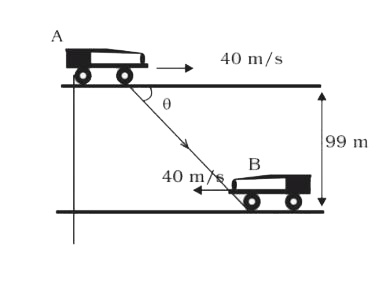
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- A train A crosses a station with a speed of 40 m/s and whitles a short...
Text Solution
|
- A train A crosses a station with a speed of 40 m/s and whitles a short...
Text Solution
|
- An observer standing at station observes frequency 219 Hz when a train...
Text Solution
|
- A man is travelling in a train towards the station with a speed of 50 ...
Text Solution
|
- A man is travelling in a train towards the station with a speed of 50 ...
Text Solution
|
- A train is moving with a unifrom speed of 33 m/ s and an observer is a...
Text Solution
|
- एक रेलगाड़ी की सीटी की आवृत्ति 360 हर्ट्ज है। जब यह रेलगाड़ी किसी स्टेशन...
Text Solution
|
- Train A and B are approaching towards each other on a parallel track 9...
Text Solution
|
- A train is moving with a uniform speed of 33 m/s and an observer is ap...
Text Solution
|