Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
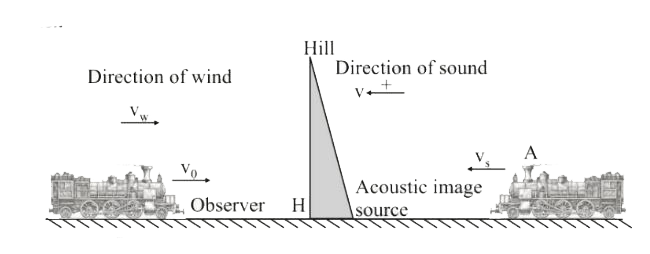
- A train approaching a hill at a speed of 40 km//hr sounds a whistle of...
Text Solution
|
- A train approaching a hill at a speed of 40 km//hr sounds a whistle of...
Text Solution
|
- A train approching a hill at a speed of 40 km//hr sounds a whitstle of...
Text Solution
|
- A train approaching a hill at a speed of 36 kmph sounds a whistle of f...
Text Solution
|
- एक ट्रेन 40 किमी / घण्टा की चाल से किसी पहाड़ी की ओर जा रही है। जब ...
Text Solution
|
- A train moving towards a hill at a spped 72 km/her sounds a whistle of...
Text Solution
|
- A train approaching a hill at a speed of 60 km//hour sounds a whistle ...
Text Solution
|
- A train approaching a hill at a speed of 40 km/hour sounds a whistle o...
Text Solution
|
- A train approaching a hill at a speed of 40 km/hour sounds a whistle o...
Text Solution
|