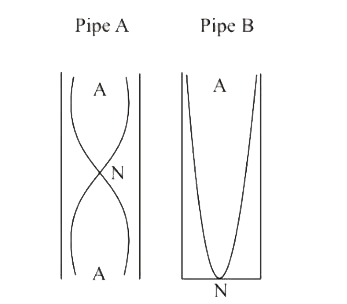
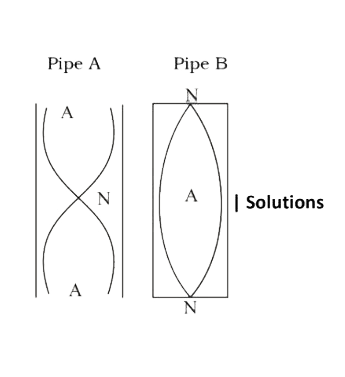
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- Two narrow cylindrical pipes A and B have the same length. Pipe A is o...
Text Solution
|
- Two narrow cylindrical pipes A and B have the same length. Pipe A is o...
Text Solution
|
- Two narrow cylindrical pipes A and B have the same length . Pipe A is ...
Text Solution
|
- The frequency of the second overtone in a pipe open at both ends is n(...
Text Solution
|
- If the frequency of first harmonic of a closed pipe is in unison with ...
Text Solution
|
- The frequency of third overtone of a pipe closed at one end , is in un...
Text Solution
|
- दो संकीर्ण बेलनाकार पाइप A तथा B समान लम्बाई के है। पाइप A दोनों स...
Text Solution
|
- Differentiate between closed pipe and open pipe at both ends of same l...
Text Solution
|
- Pipe A , with length L , and pipe B , with length 2l , both have two o...
Text Solution
|