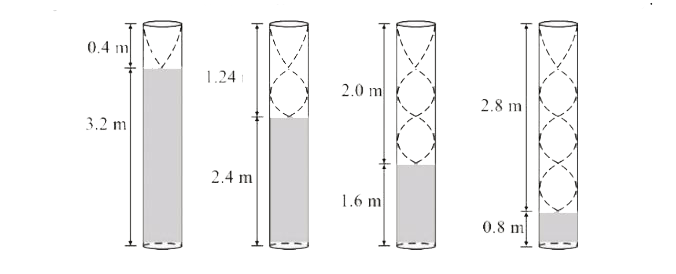
Text Solution
Verified by Experts
Recommended Questions
- A 3.6m long vertical pipe resonates with a source of frequency 212.5 H...
Text Solution
|
- A 3.6m long vertical pipe resonates with a source of frequency 212.5 H...
Text Solution
|
- A sufficiently long closed organ pipe has a small hole at its bottom ....
Text Solution
|
- The fundamental of a closed pipe is 220 Hz. If (1)/(4) of the pipe is ...
Text Solution
|
- An open pipe resonates to a frequency n1 and closed pipe to a frequenc...
Text Solution
|
- An air column in a resonace tube of length 1.5 m resonates with a sour...
Text Solution
|
- 20सेमी लंबाई के पाइप का एक सिरा बंद है। 430 Hz आवृत्ति के स्रोत्र द्व...
Text Solution
|
- 3 . 6 मी लम्बा एक ऊर्ध्वाधर पाइप 212 . 5 हर्ट्ज आवृत्ति के एक स्रो...
Text Solution
|
- एक पाइप A पर जल वेग v से प्रवेश करता है तथा पाइप के ऊर्ध्वाधर भाग में...
Text Solution
|