Two stones are through up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? Assume stones do not rebound after hitting the ground and neglect air resistance, take . ` g= 10 m//s^(2) ` (The figures are schematic and not drawn to scale)
Two stones are through up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? Assume stones do not rebound after hitting the ground and neglect air resistance, take . ` g= 10 m//s^(2) ` (The figures are schematic and not drawn to scale)
A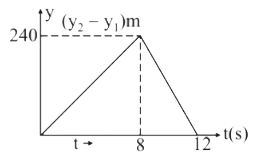

B

C

D

Text Solution
AI Generated Solution
The correct Answer is:
To solve the problem of the two stones thrown from a cliff, we need to analyze their motions and find the relative position of the second stone with respect to the first stone over time.
### Step 1: Determine the equations of motion for both stones.
**For Stone 1 (initial speed = 10 m/s):**
- Initial height (h) = 240 m
- Initial velocity (u₁) = 10 m/s (upward)
- Acceleration (a) = -g = -10 m/s² (downward)
Using the equation of motion:
\[
s_1 = u_1 t + \frac{1}{2} a t^2
\]
Substituting the values:
\[
s_1 = 10t - \frac{1}{2} \cdot 10 \cdot t^2
\]
\[
s_1 = 10t - 5t^2
\]
**For Stone 2 (initial speed = 40 m/s):**
- Initial velocity (u₂) = 40 m/s (upward)
Using the same equation of motion:
\[
s_2 = u_2 t + \frac{1}{2} a t^2
\]
Substituting the values:
\[
s_2 = 40t - 5t^2
\]
### Step 2: Calculate the time taken for each stone to hit the ground.
**For Stone 1:**
Setting the displacement equal to the height of the cliff:
\[
240 = 10t - 5t^2
\]
Rearranging gives:
\[
5t^2 - 10t - 240 = 0
\]
Dividing by 5:
\[
t^2 - 2t - 48 = 0
\]
Using the quadratic formula:
\[
t = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
Where \( a = 1, b = -2, c = -48 \):
\[
t = \frac{2 \pm \sqrt{(-2)^2 - 4 \cdot 1 \cdot (-48)}}{2 \cdot 1}
\]
\[
t = \frac{2 \pm \sqrt{4 + 192}}{2}
\]
\[
t = \frac{2 \pm 14}{2}
\]
The positive root gives:
\[
t = 8 \text{ seconds}
\]
**For Stone 2:**
Setting the displacement equal to the height of the cliff:
\[
240 = 40t - 5t^2
\]
Rearranging gives:
\[
5t^2 - 40t + 240 = 0
\]
Dividing by 5:
\[
t^2 - 8t + 48 = 0
\]
Using the quadratic formula:
\[
t = \frac{8 \pm \sqrt{(-8)^2 - 4 \cdot 1 \cdot 48}}{2 \cdot 1}
\]
\[
t = \frac{8 \pm \sqrt{64 - 192}}{2}
\]
This gives no real solution, indicating that Stone 2 will also hit the ground after 8 seconds.
### Step 3: Determine the relative position of Stone 2 with respect to Stone 1.
The relative position \( Y \) of Stone 2 with respect to Stone 1 is given by:
\[
Y = s_2 - s_1
\]
Substituting the equations:
\[
Y = (40t - 5t^2) - (10t - 5t^2)
\]
\[
Y = 40t - 10t
\]
\[
Y = 30t
\]
### Step 4: Analyze the graph of relative position over time.
- From \( t = 0 \) to \( t = 8 \) seconds, the relative position \( Y \) increases linearly as \( 30t \).
- After \( t = 8 \) seconds, Stone 1 hits the ground, and Stone 2 continues to move upward until it reaches its peak and then falls back down.
### Conclusion:
The best representation of the time variation of the relative position of the second stone with respect to the first stone will show a linear increase until \( t = 8 \) seconds, followed by a downward parabolic motion after Stone 1 hits the ground.
To solve the problem of the two stones thrown from a cliff, we need to analyze their motions and find the relative position of the second stone with respect to the first stone over time.
### Step 1: Determine the equations of motion for both stones.
**For Stone 1 (initial speed = 10 m/s):**
- Initial height (h) = 240 m
- Initial velocity (u₁) = 10 m/s (upward)
- Acceleration (a) = -g = -10 m/s² (downward)
...
Similar Questions
Explore conceptually related problems
Two stones are thrown up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m//s and 40 m//s respectively . Which of the following graph best represents the time variation of relative position of the speed stone with respect to the first ? ( Assume stones do not rebound after hitting the groumd and neglect air resistance , take g = 10 m//s^(2)) ( The figure are schematic and not drawn to scale )
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 ms?^(-1) and 30^(-1) . Verify that the graph shown in Fig. 2 ( NCT). 13 , correctly represents the time variation of the relativ e position of the second stone with respect to the first. Neglect the air resistance and assume that the stones do not rebound after hitting the ground. Taje g= 10 ms^(-2) .Give equations for the linear and curved parts of the plot. .
Two stones are thrown up simultaneously with initial speeds of u_(1) and u_(2)(u_(2)gt_(1) u_(1)) . They hit the ground after 6 s and 10 s respectively. Which graph in fig. correctly represents the time variation of Deltax=(x_(2)-x_(1)) the relative position of the second stone with respect to the first upto t=10 s? Assume that the stones do not rebound after hitting the ground.
Two stones are thrown up simultaneously from the edge of a cliff with initial speed v and 2 v . The relative position of the second stone with respect to first varies with time till both the stones strike the ground as.
One stone is projected horizontally from a 20 m high cliff with an initial speed of 10 ms^(-1) . A second stone is simultaneously dropped from that cliff. Which of the following is true?
Two stones are thrown vertically upwards simultaneously from the same point on the ground with initial speed u_(1) = 30 m//sec and u_(2) = 50 m//sec . Which of the curve represent correct variation (for the time interval in which both reach the ground) of (x_(2) - x_(1)) = the relative position of second stone with respect to first with time (t) (v_(2) - v_(1)) = the relative velocity of second stone with respect to first with time (t). Assuming that stones do not rebound after hitting.
A man standing on the edge of a cliff throws a stone straight up with initial speed (u) and then throws another stone straight down with same initial speed and from the same position. Find the relation of the speeds. The stones would have attained when they hit ground at the base of the cliff.
Recommended Questions
- Two stones are through up simultaneously from the edge of a cliff 240 ...
Text Solution
|
- Two stones are thrown up simultaneously from the edge of a cliff 240 m...
Text Solution
|
- Two stones are thrown up simultaneously from the edge of a cliff 200 m...
Text Solution
|
- किसी 200 m ऊंची खड़ी चट्टान के किनारे से दो पत्थरों को एक साथ ऊपर की ओ...
Text Solution
|
- किसी 240 मी ऊँची चोटी से एक किनारे से, दो पत्थरों को एक साथ ऊपर की और...
Text Solution
|
- Two stones are through up simultaneously from the edge of a cliff 240 ...
Text Solution
|
- Two stones are through up simultaneously from the edge of a cliff 240 ...
Text Solution
|
- Two stones are thrown up simultaneously from the edge of a cliff 240 m...
Text Solution
|
- Two stones are thrown up simultaneously from the edge of a cliff 240 m...
Text Solution
|