( i ) इस स्थिति में गुटके पर चित्र के अनुसार बल कार्य करेंगे | जहाँ mg गुटके का भार , R अभिलंब प्रतिक्रिया, `f_(k)` गतिक घर्षण बल ( गति की विपरीत दिशा में तल के समांतर ऊपर की ओर ) तथा f तल के समांतर गुटके पर नीचे की ओर लगाया गया बाह्य बल हैं | अत्वरित गति के लिए गुटके पर नेट बल शून्य होगा |
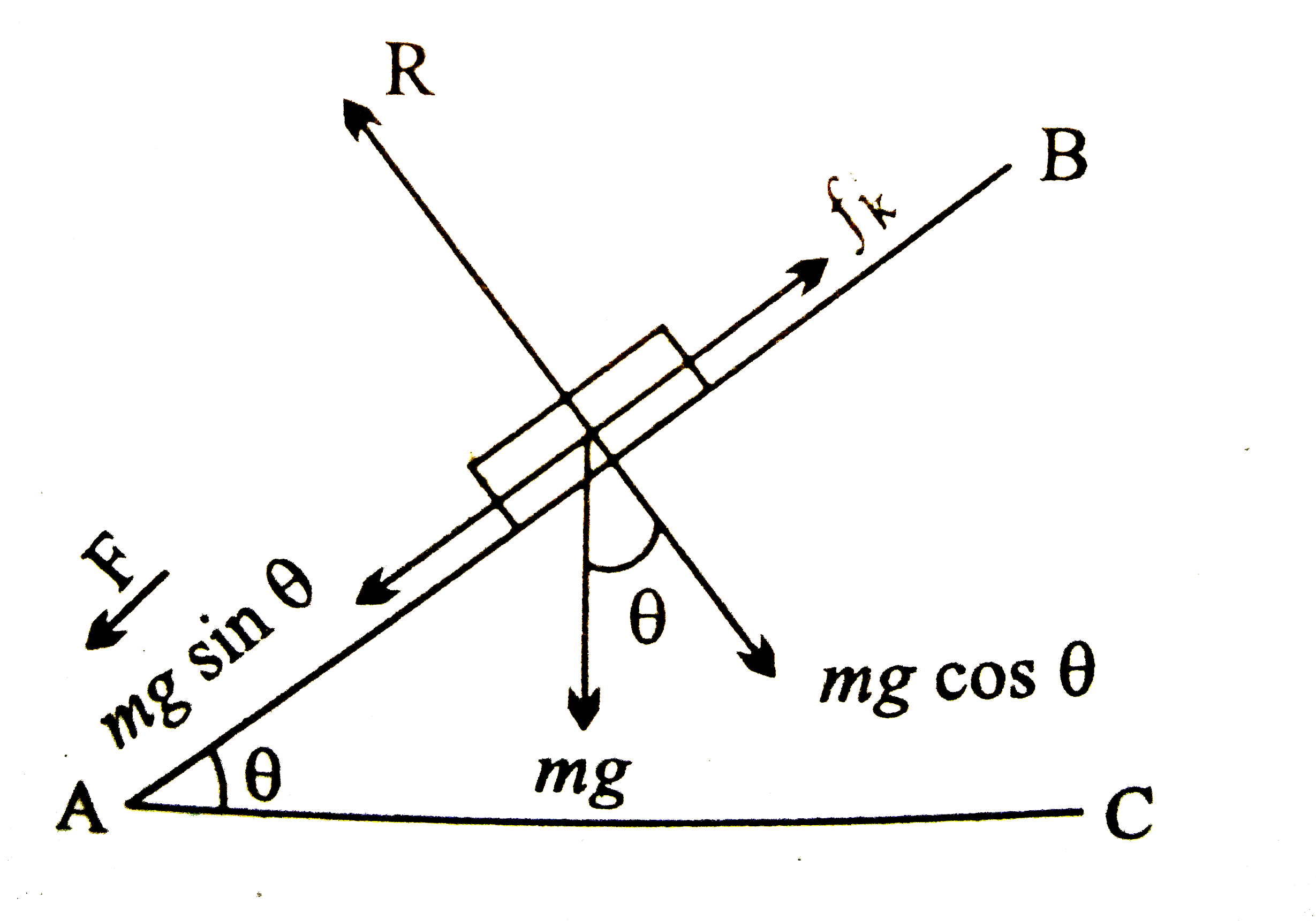
`therefore F+mg sin 30^(@)-f_(k)=0`
या `" "F=f_(k)-mg sin 30^(@)" ..(1)"`
परन्तु `f_(k)=mu_(k)R=mu_(k)mg cos 30^(@)=(sqrt3)/(sqrt2)mg cos 30^(@)`
समी. (1 ) रखने पर,
`F=(sqrt3)/(sqrt2) mg cos 30^(@)-mg sin 30^(@)`
`=(sqrt3)/(sqrt2)xx9.8-9.8=20.79-9.8` न्यूटन| (ii ) इस स्थिति में चित्र के अनुसार,
`mg sin 30^(@)+f_(k)-F=0`
या `F=mg sin 30^(@)+f_(k)`

`=mg sin 30^(@)+(sqrt3)/(sqrt2)mg cos 30^(@)`
`=2xx9.8xx(1)/(2)+(sqrt3)/(sqrt2)xx2xx9.8xx(sqrt3)/(2)`
`=9.8+20.79=30.59` न्यूटन |
(iii ) शक्ति `P=Fv` से,
`(P_(1))/(P_(2))=(F_(1))/(F_(2))xx(v_(1))/(v_(2))" में "v_(1)=v_(2)`
`therefore" "(P_(1))/(P_(2))=(F_(1))/(F_(2))=(10.99)/(30.59)=(0.036)/(1)`.

