Find the components of a vector `vecR` along two straight lines stiuated at both sides of the vector`vecR` making angles `alpha` and `beta` with it.

Explanation

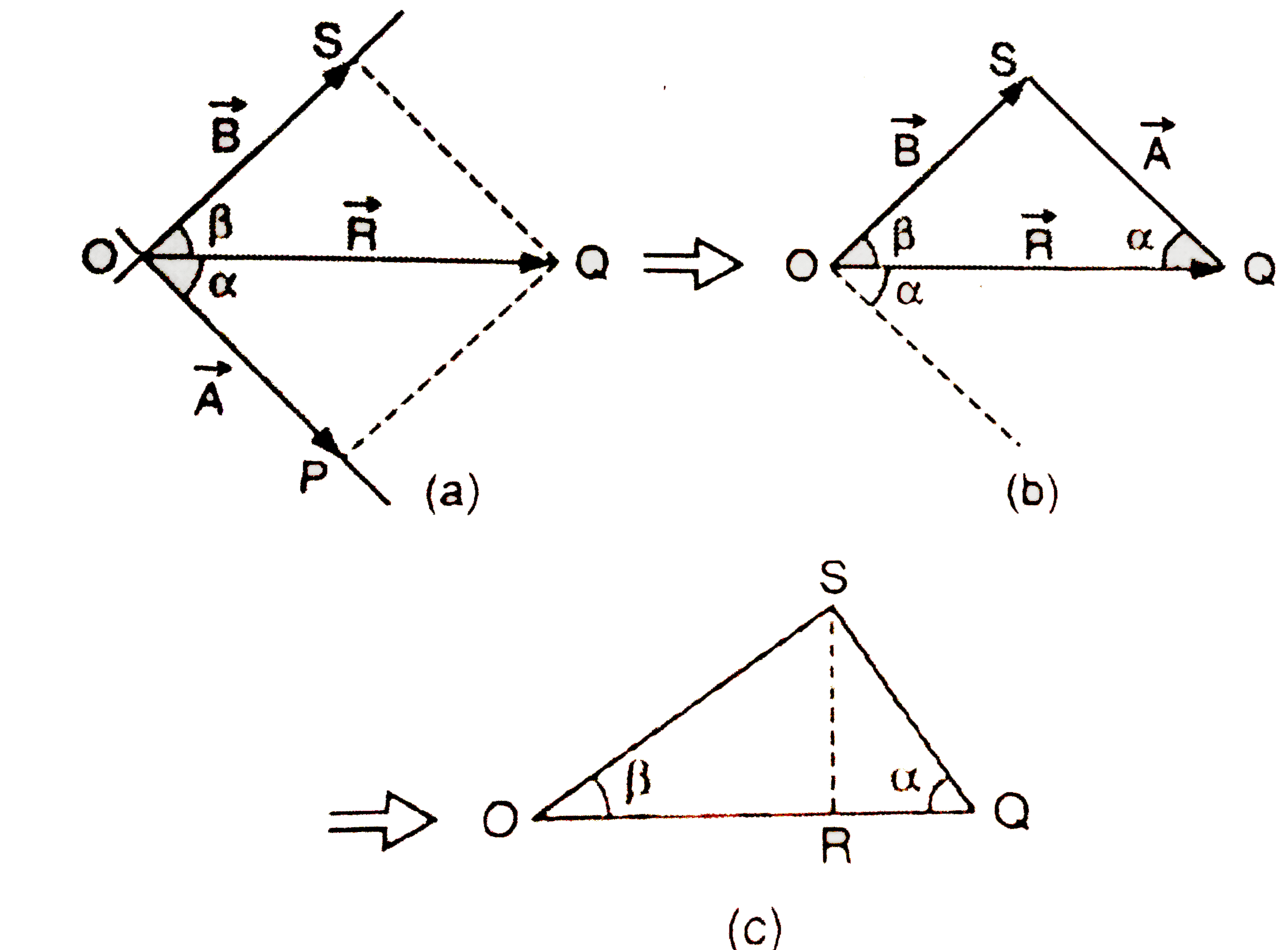
Since the components `vecA and vecB` of the given
vector`vecR` are choose in the given directions, `vecR` is the resultant of
`vecA` and `vecB`, then , `vecR = vecA + vecB`. Hence, R is repersented by the
diagonal OQ of the square ` OPQS` where the component vectors `vecA`
and `vecB` respresented by the adjacent sides OP and OS
respectivcely according to the parallelogram law of vectors.
Then we convert the parallelorgam OSQP to the vectors triangle
OSQ which represents the vectos `vecR, vecA and vecB` as shown in the
Fig. 3.40 (a). By converting to a scalar triangle OSQ as shown in the Fig. 3.40 (c), we can write
`OQ = OS cos beta + SQ cos alpha" " ....(i)`
and `SR = OS sin beta = SQ sin alpha " "......(ii)`
Solving the Eqs. (i) and (ii), we have
`QS = |vecA| = (OQ sin beta)/(sin (alpha + beta))= ( R sin beta)/( sin( alpha + beta))`
and `OS = |vecB| = (R sin alpha)/(sin (alpha + beta))`

Alternate solution
Using Lami,s theorm, we have
`(|vecA|)/(sin beta)= (|vecB|)/( sin alpha) = (|vecR|)/(sin { 180^(@) - (alpha-beta)})`

This yields `|vecA|= (|vecR| sin beta)/(sin (alpha + beta)) and |vecB| = (|vecR| sin alpha)/(sin (alpha+ beta))`