Home
Class 11
PHYSICS
ABCDEF is a regular hexagon, Fig. 2 (c )...

`ABCDEF` is a regular hexagon, Fig. 2 (c ) .65. What is the value of
` (vec (AB) + vec (AC) + vec (AD) + vec (AE) + vec (AF) ?`
.

A

`4 vecAO`

B

`3 vecAD`

C

`8 vecAD`

D

zero

Text Solution

Verified by Experts

The correct Answer is:
B
Use `" "vecAB = vecAO + vecOB`
`" "vecAC = vecAO + vecOC`
`" "vecAD = vecAO + vecOD`
`" "vecAE = vecAO + vecOE`
`" "vecAF = vecAO + vecOF`
Promotional Banner

Topper's Solved these Questions

  • VECTORS

    GRB PUBLICATION|Exercise MORE THAN ONE CHOICE IS CORRECT|15 Videos

  • VECTORS

    GRB PUBLICATION|Exercise ASSERTION- REASON|1 Videos

  • VECTORS

    GRB PUBLICATION|Exercise PROBLEMS FOR PARCTICE|23 Videos

  • UNITS AND DIMENSIONS

    GRB PUBLICATION|Exercise Link Compression|6 Videos

Similar Questions

Explore conceptually related problems

ABCDEF is a regular hexagon with point O as centre. The value of vec(AB)+vec(AC)+vec(AD)+vec(AE)+vec(AF) is

In a regular hexagon ABCDEF,vec AE

In Fig. ABCDEF is a ragular hexagon. Prove that vec(AB) +vec(AC) +vec(AD) +vec(AE) +vec(AF) = 6 vec(AO) .

If ABCDE is a pentagon, then vec(AB) + vec(AE) + vec(BC) + vec(DC) + vec(ED) + vec(AC) is equal to

ABCD is a parallelogram Fig. 2 (c ) .64. AC and (BD) are its diagonals. Show that (a) vec (AC) +vec (BD) =2 vec (BC) (b) vec (AC) - vec (BD) =2 vec (AB) .

ABCDEF be a regular hexagon in the xy-plane and vec AB=4hat i then vec CD=

ABCDEF is a regular hexagon with centre a the origin such that vec(AB)+vec(EB)+vec(FC)= lamda vec(ED) then lamda = (A) 2 (B) 4 (C) 6 (D) 3

ABCDEF is a regular hexagon.Find the vector vec AB+vec AC+vec AD+vec AE+vec AF in terms of the vector vec AD

In a regular hexagon ABCDEF, prove that vec(AB)+vec(AC)+vec(AD)+vec(AE)+vec(AF)=3vec(AD)

GRB PUBLICATION-VECTORS-OBJECTIVE QUESTIONS
  1. A particle is given successive displacments. Which of the followin...

    Text Solution

    |

  2. An expression which cannot be defined meaningfully among vectors is :

    Text Solution

    |

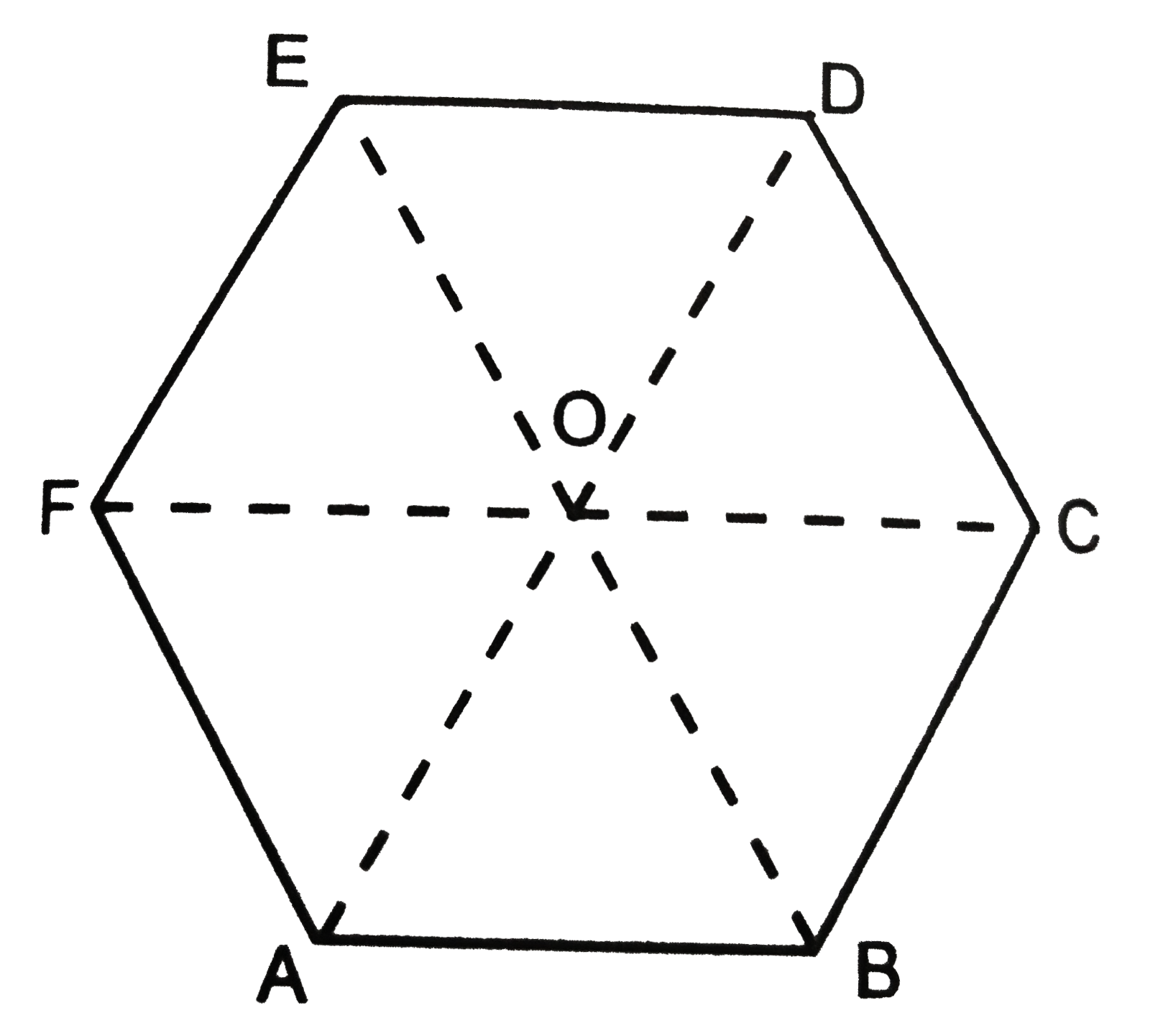
  3. ABCDEF is a regular hexagon, Fig. 2 (c ) .65. What is the value of ...

    Text Solution

    |

  4. In the regular hexagon shown in Fig. 3.51, vecAB + vecBC + vecCD+ ve...

    Text Solution

    |

  5. In the regular hexagon shown in fig.3.51, vecAO+vecBO + vecCO+vecDO +...

    Text Solution

    |

  6. For vectors vecA and vecB, (vecA + vecB). (vecA xx vecB) will be :

    Text Solution

    |

  7. Minimum number of two coplanar vectors of equal magnitude whose v...

    Text Solution

    |

  8. Assertion: The minimum number of non-coplanar Vectors whose sum can be...

    Text Solution

    |

  9. In Fig. 3.52, D is the mid-point of vecBC Which of the following re...

    Text Solution

    |

  10. Sum of magnetic of two forces acting on a body is 15 N. The resulta...

    Text Solution

    |

  11. Resultant of two forces vecF(1) and vecF(2) has magnitude 50 N. Th...

    Text Solution

    |

  12. vecA, vecB and vecC are vectors such that vecC= vecA + vecB and vecC...

    Text Solution

    |

  13. A person walks along the path shown in Fig. 3.53. The path from B...

    Text Solution

    |

  14. ABCD is parallelogram vecA, vecB, vecC and vecD are the position vec...

    Text Solution

    |

  15. A lion is at some instant a position A(2m, 6m ,-1m) and a goat is...

    Text Solution

    |

  16. A vector vecA points vertically upward and vecB points towards north. ...

    Text Solution

    |

  17. A parallelogram is fromed withveca and vecb as the sides let vecd...

    Text Solution

    |

  18. vecA and vecB and vectors expressed as vecA = 2hati + hatj and vecB = ...

    Text Solution

    |

  19. The vector area of triangle position vectors of whose vertices are vec...

    Text Solution

    |

  20. Area of the parallelogram formed by vectors vecA = hati + 2hatj+ 4 ...

    Text Solution

    |