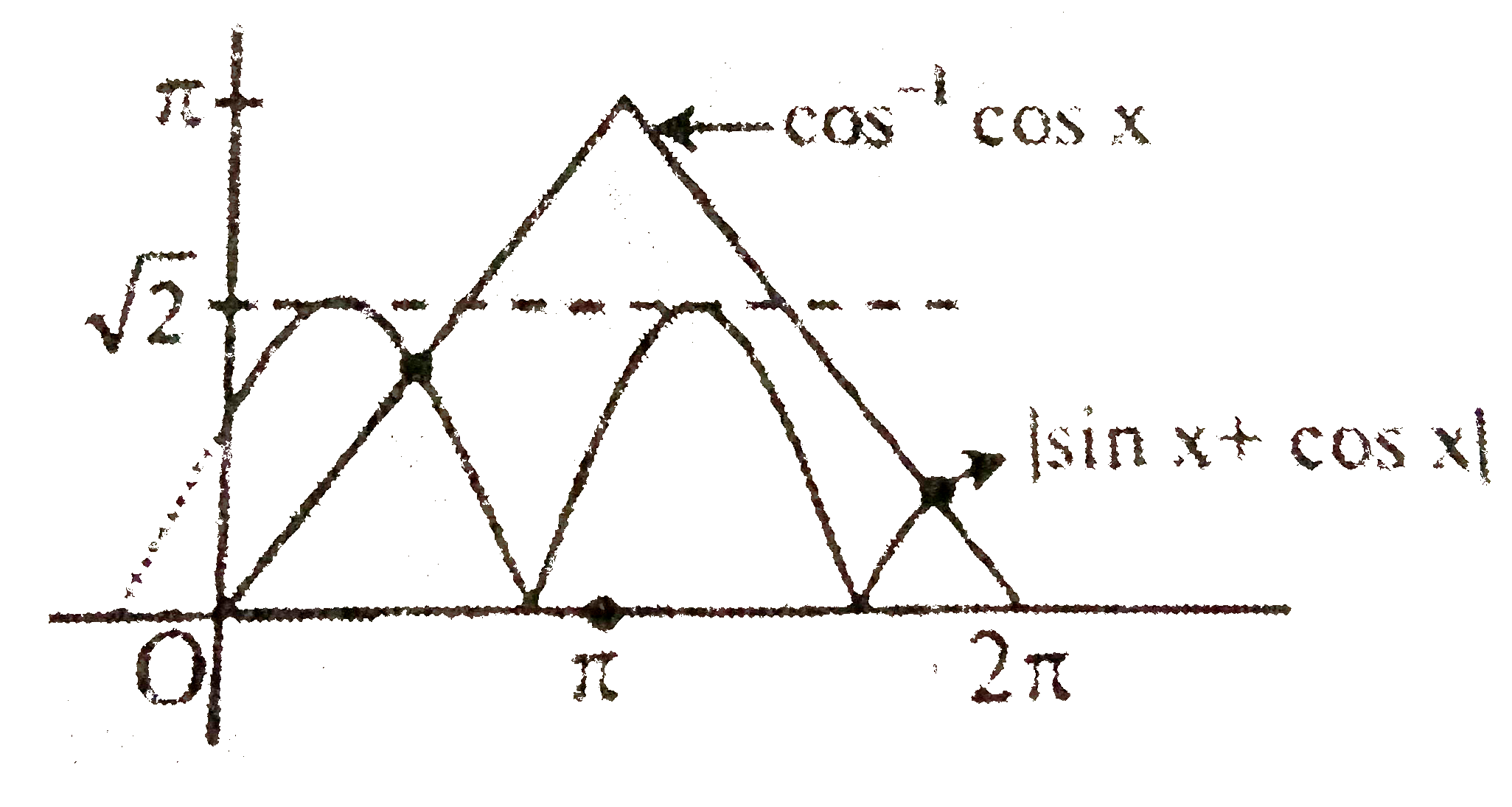Home
Class 12
MATHS
If cos^(-1)(cosx)=sqrt(1sin2x)AAxepsi(0,...

If `cos^(-1)(cosx)=sqrt(1sin2x)AAxepsi(0,2pi),` then no. of solution =

A

2

B

4

C

3

D

5

Text Solution

Verified by Experts

The correct Answer is:
A

`sqrt(sin2x)=|sin x+ cos x|`
`=sqrt(2)|sin(x+(pi)/(4))|`
Promotional Banner

Topper's Solved these Questions

  • MOCK TEST 4

    CAREER POINT|Exercise MATHS|30 Videos

  • MOCK TEST 6

    CAREER POINT|Exercise Part (C) (MATHS)|30 Videos

Similar Questions

Explore conceptually related problems

Solve cos^(-1)(cosx)>sin^(-1)(sinx),x in [0,2pi]

If sqrt(3) ( cos^2 x) = ( sqrt(3)-1) cos x +1, the numbers of solution of the given equation when x in [0,pi/2] is

Number of solutions of the equation cos ec^(-1)(cos ecx)=sin x. in [-2 pi,2 pi] is 'a' and number of solutions of cos ec^(-1)(cos ecx)=sqrt(sin x) in this interval is 'b' then sqrt(a+b) is

If x in[0,2 pi] for which 2cos x<=|sqrt(1+sin2x)-sqrt(1-sin2x)|<=sqrt(2) has solution set x in[(lambda pi)/(4),(mu pi)/(4)] then value of lambda+mu is

int(cos2x)/((e^(-x)+cosx)sqrt(1+sin2x))dx,x in(0,(pi)/(2)) is equal to

If (sqrt(1+cosx)+sqrt(1-cosx))/(sqrt(1+cosx)-sqrt(1-cosx))=cot(a+x/2) and x in (pi,2pi) then 'a' is equal to :

Consider the function f(x)=(sqrt(1+cos x)+sqrt(1-cosx))/(sqrt(1+cosx)-sqrt(1-cos x)) then Q. If x in (pi, 2pi) then f(x) is

The total number of solutions of cos x= sqrt(1- sin 2x) in [0, 2pi] is equal to

If 2cosx(4sin(pi/4+x) sin(pi/4-x)-1)=1 then for x in [0,pi] then the number of solution s is n ,and the sum of solutions is s then find the value of (n,s)

CAREER POINT-MOCK TEST 5-Part (C) (MATHS)
  1. Total number of integral values of 'a' so that x^(2)-(a+1)x+a-1=0 has ...

    Text Solution

    |

  2. If a,b,c,d are such unequal real numbers that (a^(2)+b^(2)+c^(2))p^(2)...

    Text Solution

    |

  3. If (x) donotes the greates integer lex, then the value of int(4)^(10)...

    Text Solution

    |

  4. The area of the portion of the circle x^(2)+y^(2)=1 which lies inside ...

    Text Solution

    |

  5. Solution of the differential equation x dy -y dx = 0 represents-

    Text Solution

    |

  6. k=lim(xtooo)[(sum(k=1)^(1000)(x+k)^(m))/(x^(m)+10^(1000))] (mgt101) is...

    Text Solution

    |

  7. if roots of ax^(2)+bx+c=0 where epsiR^(+), are two positive consecutiv...

    Text Solution

    |

  8. If cos^(-1)(cosx)=sqrt(1sin2x)AAxepsi(0,2pi), then no. of solution =

    Text Solution

    |

  9. For a what value (s) of a, will the two points (1,a,1) and (-3,0,a) li...

    Text Solution

    |

  10. The number of integer values of x for which the inequality "log "(10) ...

    Text Solution

    |

  11. If three vectors (sec^(2)A) hati+hatj+hatk, hati+(sec^(2)B)hatj+hatk,...

    Text Solution

    |

  12. Maximum value of the expression (10x^(12))/(x^(24)+2x^(12)+3x^(16)+...

    Text Solution

    |

  13. if f be a differentiable function such that f(x) =x^(2)int(0)^(x)e^(-t...

    Text Solution

    |

  14. For what values of a, m and b, Lagrange's mean value theerorem is appl...

    Text Solution

    |

  15. The value of x for which f(x)=(sin.({x})/({x})+cos.({x})/({x})) is max...

    Text Solution

    |

  16. If l^r(x) means logloglog.......x being repeated r times, then int [ (...

    Text Solution

    |

  17. Consider the non-empty set consisting of children in a family and a r...

    Text Solution

    |

  18. u(n) = |{:(1,,k,,k),(2n,,k^(2)+k+1,,k^(2)+k),(2n-1,,k^(2),,k^(2)+k+1):...

    Text Solution

    |

  19. Let (p) x be a polynomial of degree 4 having extemum at x= 1,2 and lim...

    Text Solution

    |

  20. The mean of 50 observation is 36. if two observation 30 and 42 are to ...

    Text Solution

    |