Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
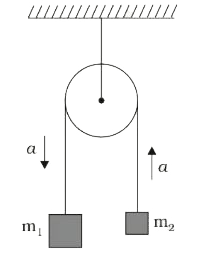
- Two bodies of masses m1 and m2( < m1) are connected to the ends of a ...
Text Solution
|
- Three blocks of masses m1, m2 and m3 are connected as shown in the fig...
Text Solution
|
- Find the acceleration of centre of mass of the blocks of masses m1, m2...
Text Solution
|
- Two bodies of masses m1 and m2(
Text Solution
|
- Two blocks of masses m1 and m2 (m1 gt m2) in contact with each other...
Text Solution
|
- If two masses m1 and m2 (m1 gt m2) tied to string moving over a fricti...
Text Solution
|
- In the arrangement shown in the figure all surfaces are frictionless, ...
Text Solution
|
- m1,m2 व m3 द्रव्यमान के तीन ब्लॉक प्रदर्शित चित्र में घर्षणहीन मेज पर...
Text Solution
|
- Three blocks of masses m1, m2 and m3 are connected as shown in the fig...
Text Solution
|