A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
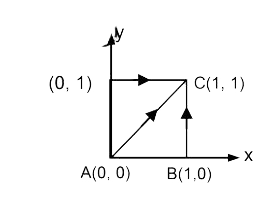
- A particle of mass m moves from A to C under the action of force vecF ...
Text Solution
|
- Force acting on a particle moving in the x-y plane is vecF=(y^2hati+xh...
Text Solution
|
- Force acting on a particle moving in the x-y plane is vecF=(y^2hati+xh...
Text Solution
|
- A particle is moved along the different paths OAC, OBC & ODC as shown ...
Text Solution
|
- A particle of mass M moves with constant speed along a circular path o...
Text Solution
|
- A particle of mass 'm' moves with a constant speed along a circular pa...
Text Solution
|
- A force vecF=xhati+y^(2)hatjN acts on a particle and the particle move...
Text Solution
|
- A particle of mass m moves from A to C under the action of force vecF ...
Text Solution
|
- A particle of mass m moves from A to C under the action of force vecF ...
Text Solution
|