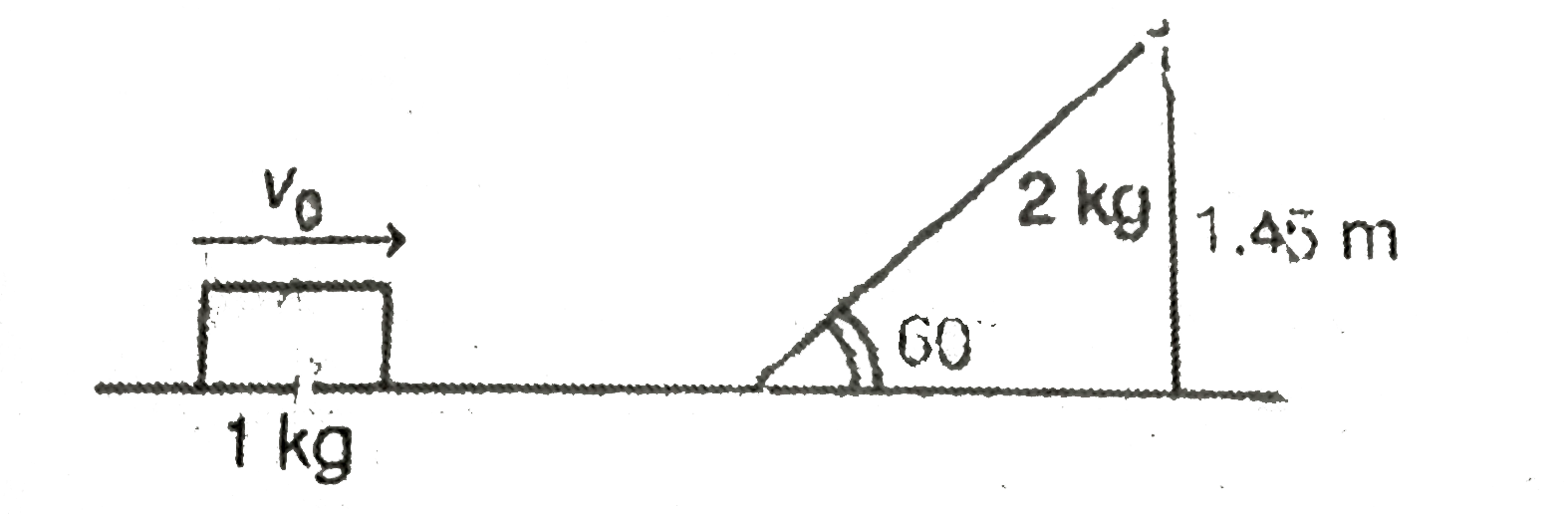A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A block of mass 1 kg is moving towards a movablen vedge of amss 2 kg a...
Text Solution
|
- All surfaces shown in figure are smooth. Wedges of mass 'M' is free to...
Text Solution
|
- A smooth wedge of mass M rests on a smooth horizontal surface. A block...
Text Solution
|
- A block of mass m is pushed towards the movable wedge of mass M and he...
Text Solution
|
- A wedge (inclination theta = 30^(@) from horizontal) is moving with an...
Text Solution
|
- A block of mass 1 kg is moving towards a movablen vedge of amss 2 kg a...
Text Solution
|
- A block of mass 1 kg is moving towards a movablen vedge of amss 2 kg a...
Text Solution
|
- A block of mass 1 kg is moving towards a movablen vedge of amss 2 kg a...
Text Solution
|
- In the arrangement as shown, block A of mass 3 kg moves towards left w...
Text Solution
|