Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
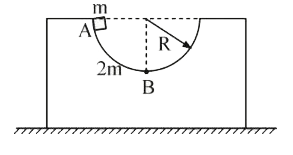
- In the system shown in figure, mass m is released from rest from posit...
Text Solution
|
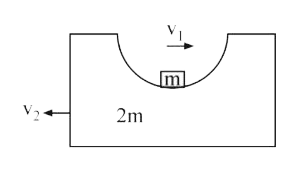
- A particle A of mass m is situated at highest point of wedge B of mass...
Text Solution
|
- A particle of mass m, kinetic energy K and momentum p collision head o...
Text Solution
|
- A block A of mass M on an inclined surface and a small weight B of mas...
Text Solution
|
- In the system shown in figure, mass m is released from rest from posit...
Text Solution
|
- In the system shown in figure, mass m is released from rest from posit...
Text Solution
|
- If the mass and kinetic energy of a particle are m and E respectively,...
Text Solution
|
- In the system shown in figure, mass m is released from rest from posit...
Text Solution
|
- In the system shownn in figure mass m is released from position A. Sup...
Text Solution
|