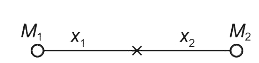A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Consider a two-particle system with particles having masses m1 and m2...
Text Solution
|
- Consider a two particle system with the prticles having masses m1 and ...
Text Solution
|
- Consider a two particle system with particles having masses m1 and m2 ...
Text Solution
|
- Consider a system of two particles having masses m(1) and m(2) . If th...
Text Solution
|
- A system of two particles is having masses m(1) and m(2) . If the part...
Text Solution
|
- Consider a two-particle system with particles having masses m1 and m2...
Text Solution
|
- Consider a two-particle system with the particle having masses m(1) an...
Text Solution
|
- Consider a two particle system with particles having masses m(1)andm(2...
Text Solution
|
- Consider a two particle system with the particles having masses m1 and...
Text Solution
|