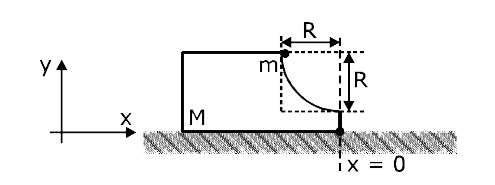
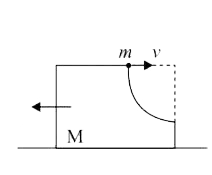
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- A block of mass M has a circular cut with a frictionless surface as sh...
Text Solution
|
- A block of mass m is placed at rest on a smooth wedge of mass M placed...
Text Solution
|
- In the system shown all the surfaces are frictionless while pulley and...
Text Solution
|
- A block of mass m(1) rests on a horizontal table. A string tied to the...
Text Solution
|
- A block of mass m rests on a wedge of mass M which, in trun, rests on ...
Text Solution
|
- For the figure shown, block of mass m is released from the rest. Find ...
Text Solution
|
- A block of mass M is placed on the top of a bigger block of mass 10 M ...
Text Solution
|
- A small cube of mass m slides down a circular path of radius R cut int...
Text Solution
|
- A block of mass M has a circular cut with a frictionless surface as sh...
Text Solution
|