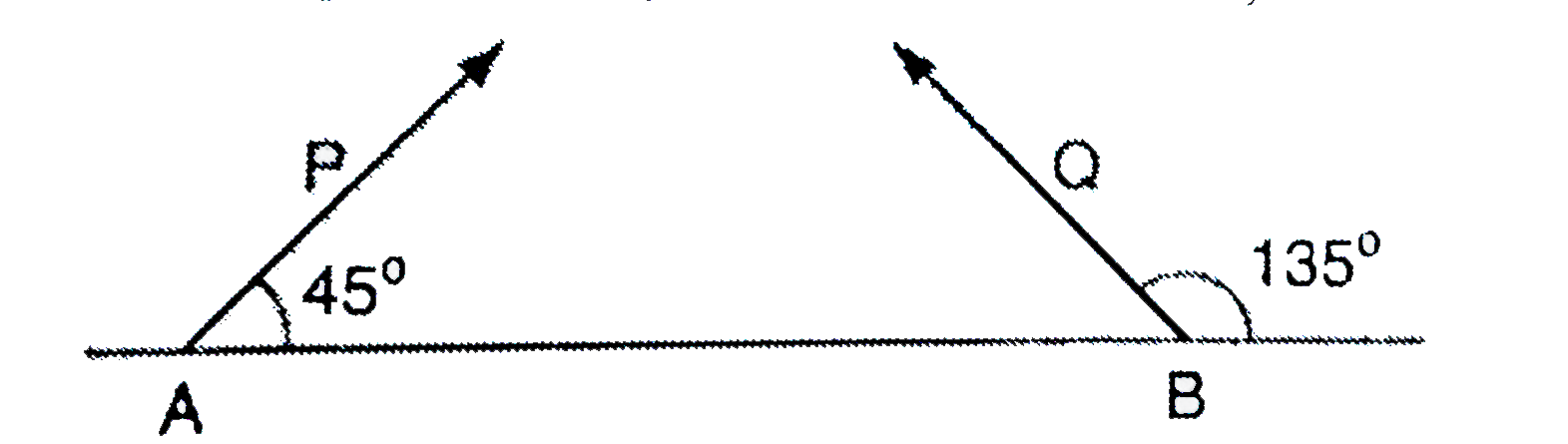
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- Particles P and Q of mass 20g and 40g respectively are simu ltaneously...
Text Solution
|
- Particles P and Q of mass 20g and 40g respectively are simu ltaneously...
Text Solution
|
- A particle is projected from a point P with a velocity v at an angle t...
Text Solution
|
- Particles P and Q of masses 20g and 40g, respectively, are projected f...
Text Solution
|
- Two particles P & Q are projected simultaneously from a point O on a l...
Text Solution
|
- A particle is projected from horizontal making an angle of 53^(@) with...
Text Solution
|
- Particles P and Q of mass 20g and 40g respectively are simu ltaneously...
Text Solution
|
- To particles P and Q are initially 40 m apart P behind Q. Particle P s...
Text Solution
|
- A particle is projected with velocity u at an angle alpha from a point...
Text Solution
|