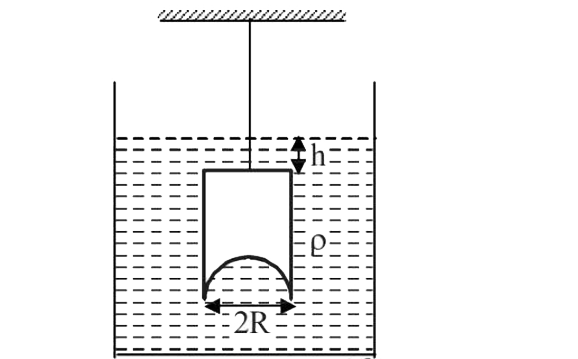
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- A hemispherical portion of radius R is removed from the bottom of a cy...
Text Solution
|
- Find the moment of inertia of a solid cylinder of mass M and radius R ...
Text Solution
|
- A hemispherical portion of radius R is removed from the bottom of a cy...
Text Solution
|
- In the figure shown, the heavy cylinder (radius R) reasting on a smoot...
Text Solution
|
- A hemispherical portion of radius R is removed from the bottom of a cy...
Text Solution
|
- A cylinder of radius R, height H and density simga has a hemispherical...
Text Solution
|
- A cylinder vessel containing a liquid of density rho is closed by a sm...
Text Solution
|
- A cylindrical vessel of radius r is filled with a homogeneous liquid u...
Text Solution
|
- A conical portion of radius R and height H is removed from the bottom ...
Text Solution
|