A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- A liquid of density 900 kg//m^3 is filled in a cylindrical tank o...
Text Solution
|
- mass m of a liquid rises inside a capillary of radius r. The mass of f...
Text Solution
|
- Shown in the figure is a container whose top and botoom diameters are ...
Text Solution
|
- A tank 5 m high is half filled with water and then is filled to top wi...
Text Solution
|
- A liquid of density 900(kg)/(m^(3)) is filled in a cylindrical tank of...
Text Solution
|
- A cylindrical tank of height 2 m is open at the top and has a radius 5...
Text Solution
|
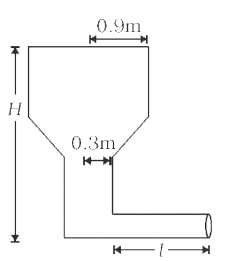
- एक बेलनाकार टंकी जिसकी ऊपरी त्रिज्या 0.9 मी तथा निचली त्रिज्या 0.3 मी ...
Text Solution
|
- A cylindrical tank of height 0.4m is open at the top and has a diamete...
Text Solution
|
- mass m of a liquid rises inside a capillary of radius r . The mass of ...
Text Solution
|