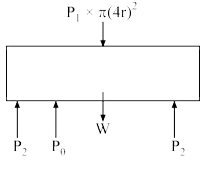
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- A cylindrical tank has a hole of diameter 2r in its bottom. The hole i...
Text Solution
|
- A cylindrical tank has a hole of diameter 2r in its bottom. The hole i...
Text Solution
|
- A cylindrical tank has a hole of diameter 2r in its bottom. The hole i...
Text Solution
|
- A cylindrical tank has a hole of diameter 2r in its bottom. The hole i...
Text Solution
|
- A cylindrical tank of height H is open at the top end and it has a rad...
Text Solution
|
- A wooden cylinder of diameter 4 r, height H and density rho//3 is kept...
Text Solution
|
- A wooden cylinder of diameter 4 r, height H and density rho//3 is kept...
Text Solution
|
- A wooden cylindrical of diameter 4r, height h and density rho//3 is ...
Text Solution
|
- A cylindrical tank of height 0.4m is open at the top and has a diamete...
Text Solution
|