Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
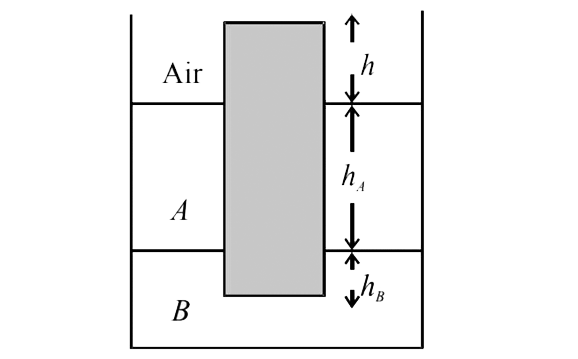
- A uniform solid cylinder of density 0.8g//cm^3 floats in equilibrium i...
Text Solution
|
- A uniform solid cylinder of density 0.8g//cm^3 floats in equilibrium i...
Text Solution
|
- Two non-mixing liquids of densities rho and (n gt1) are put in a conta...
Text Solution
|
- two cylinders A and B are of the same dimensions but of different mate...
Text Solution
|
- एक एकसमान ठोस बेलन, जिसका घनत्व 0.8" ग्राम/सेमी"^(3) है, दो अमिश्रित द...
Text Solution
|
- Two non-mixing liquids of densities rho and nrho(ngt1) are put in a co...
Text Solution
|
- A solid floats in liquid A with half its volume immersed and in liquid...
Text Solution
|
- Two non -mixing liquids of densities rho and np (ngt1) are put in cont...
Text Solution
|
- Two non-mixing liquids of densities rho and n rho ( n gt 1) are put in...
Text Solution
|