Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
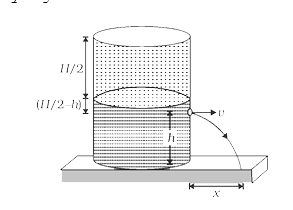
- A container of large uniform cross sectional area A, resting on horizo...
Text Solution
|
- A container of large uniform cross-sectional area A resting on a horiz...
Text Solution
|
- A container of large uniform cross-sectional area A resting on a horiz...
Text Solution
|
- A container of large uniform cross-sectional area A resting on a horiz...
Text Solution
|
- A container of large uniform cross-sectional area A resting on a horiz...
Text Solution
|
- A container of large uniform cross sectional area A resting on a horiz...
Text Solution
|
- A container of a large uniform cross-sectional area A resting on a hor...
Text Solution
|
- A container of cross-section area A resting on a horizontal surface, h...
Text Solution
|
- A vessel of large uniform cross-sectional area resting on a horizontal...
Text Solution
|