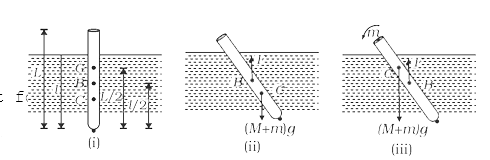Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A wooden stick of length L, radius R and density rho has a small metal...
Text Solution
|
- A uniform cube of mass M is floating on the surface of a liquid with t...
Text Solution
|
- A wooden stick of length L , radius R and density rho has a small meta...
Text Solution
|
- A massless stick of length L is hinged at one end and a mass m attache...
Text Solution
|
- A needle of length l and density rho will float on a liquid of surface...
Text Solution
|
- लकडी की एक छड़ जिसकी लम्बाई L, त्रिज्या R तथा घनत्व rho है, के एक सिरे ...
Text Solution
|
- An object of mass m is floating in a liquid of density sigma. If the o...
Text Solution
|
- rho ঘনত্বযুক্ত V আয়তনের একটি বস্তু sigma ঘনত্বের তরলে ভাসছে।
Text Solution
|
- When a body of density rho and volume V is floating in a liquid of den...
Text Solution
|