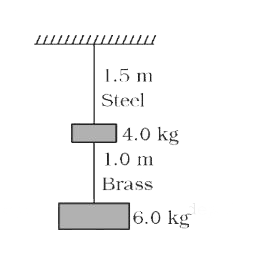Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two wires of diameter 0.25 cm, one made of steel and the other made of...
Text Solution
|
- Two wires of diameter 0.25 cm , one made of steel and other made of br...
Text Solution
|
- Young's modulus of brass and steel are 10 xx 10^(10) N//m and 2 xx 10^...
Text Solution
|
- Compute the elongation of the steel wire and brass wire in the given G...
Text Solution
|
- 0.25 cm व्यास कि दो तार, जिनमे एक इस्पात का तथा दूसरा पीतल का है, च...
Text Solution
|
- 0.25 सेमी व्यास के दो तार , जिनमे एक इस्पात का तथा दूसरा पीतल का है ,...
Text Solution
|
- The Young's modulus of brass and steel are respectively 1.0 xx 10^(11)...
Text Solution
|
- Two wires of diameter 0.25 cm, one made of steel and the other made of...
Text Solution
|
- If the ratio of lengths, radii and Young's modulus of steel and brass ...
Text Solution
|