Text Solution
Verified by Experts
Recommended Questions
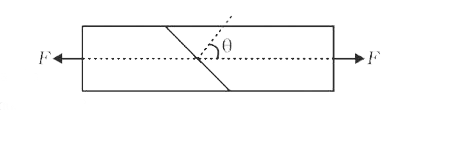
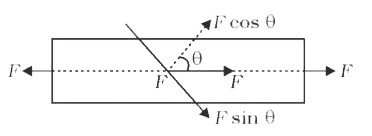
- A bar of cross-section A is subjected to equal and opposite tensile fo...
Text Solution
|
- A bar of cross section A is subjected to equal and opposite tensile fo...
Text Solution
|
- Consider a long steel bar under a tensile stress due to forces F, acti...
Text Solution
|
- A bar of cross section A is subjected to equal and opposite tensile fo...
Text Solution
|
- A bar of cross section A is subjected to equal and opposite tensile fo...
Text Solution
|
- A bar of cross section A is subjected to equal and opposite tensile fo...
Text Solution
|
- A bar of cross-section A is subjected to equal and opposite tensile fo...
Text Solution
|
- A bar of cross-section A is subjected two equal and opposite tensile f...
Text Solution
|
- Consider a long steel bar under a tensile stress due to force F acting...
Text Solution
|