A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- Two rods each of length L(2) and coefficient of linear expansion alpha...
Text Solution
|
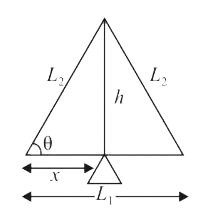
- An isosceles triangle is formed with a thin rod of length l(1) and coe...
Text Solution
|
- A composite bar of length L = L(1) + L(2) is made up from a rod of mat...
Text Solution
|
- Two rods of length l(1) and l(2) are made of material whose coefficien...
Text Solution
|
- Two rods of lengths L(1) and L(2) are welded together to make a compos...
Text Solution
|
- Two rods having length l(1) and l(2), made of materials with the linea...
Text Solution
|
- Two rods each of length L(2) and coefficient of linear expansion alpha...
Text Solution
|
- Two metal rods of lengths L(1) and L(2) and coefficients of linear exp...
Text Solution
|
- Two rods of length L(1) and L(2) are made of materials of coefficients...
Text Solution
|