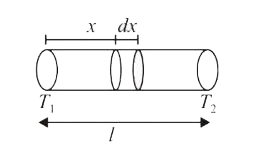
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A rod of length l and cross-section area A has a variable thermal con...
Text Solution
|
- Four identical rods AB, CD, CF and DE are joined as shown in figure. T...
Text Solution
|
- A rod of length l and cross sectional area A has a variable conductivi...
Text Solution
|
- A rod of length L with sides fully insulated is made of a material who...
Text Solution
|
- Three rods of same cross-section but different length and conductivity...
Text Solution
|
- A rod of length l and cross-section area A has a variable thermal cond...
Text Solution
|
- लम्बाई L तथा अनुप्रस्थ - क्षेत्रफल A वाली छड़ का एक सिरा T(1) तापमान व...
Text Solution
|
- Constant temperature of ends are T(1) and T(2) (where T(1)gtT(2)) for ...
Text Solution
|
- An amount of heat passing through a metallic rod in time t is given by...
Text Solution
|