A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- Assuming the Sun to be a spherical body of radius R at a temperature o...
Text Solution
|
- Assuming the Sun to be a spherical body of radius R at a temperature o...
Text Solution
|
- Assuming the sun to have a spherical outer surface of radius r radiati...
Text Solution
|
- Compute the surface temperature of the sun from the following data: Di...
Text Solution
|
- सूर्य को ताप T पर त्रिज्या R का गोला मानने पर इससे r दूरी पर पृथ्वी (त...
Text Solution
|
- r denotes the distance between the sun and the earth. Assume that the ...
Text Solution
|
- If the Sun is a sphere of radius R whose surface temperature is TK and...
Text Solution
|
- Assuming the sun to have a sphericakl outer surface of radius r radiat...
Text Solution
|
- If the temperature of sun were to increase from T to 2T and its radius...
Text Solution
|
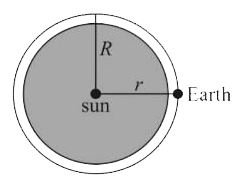 `=(sigmaT^(4)xx4piR^(2))/(4pir^(2))=(sigmaT^(4)xxR^(2))/(r^(2))`
`=(sigmaT^(4)xx4piR^(2))/(4pir^(2))=(sigmaT^(4)xxR^(2))/(r^(2))`