Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
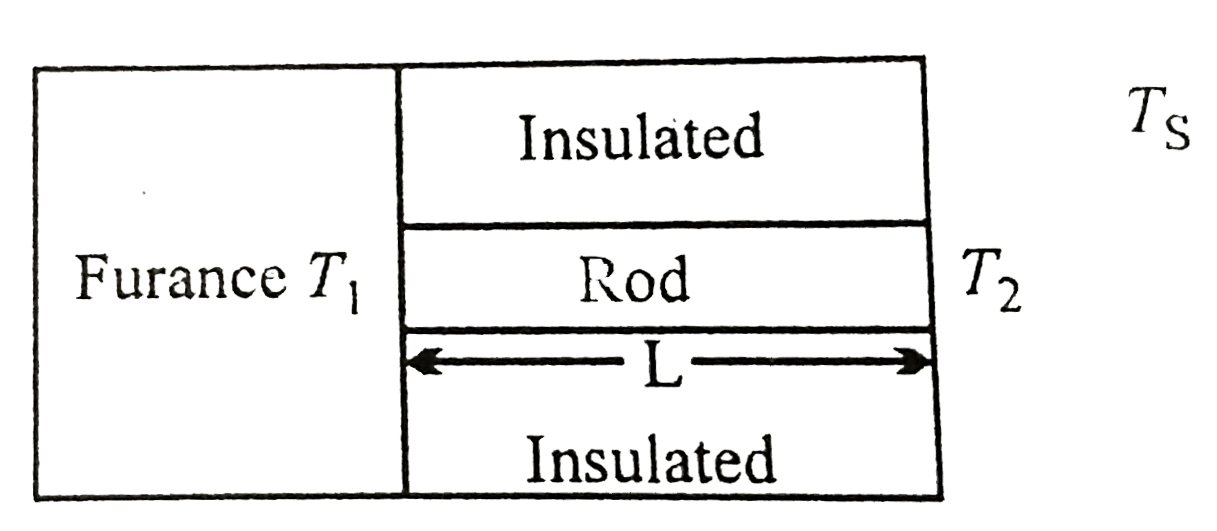
- One end of rod of length L and cross-sectional area A is kept in a fur...
Text Solution
|
- Four identical rods AB, CD, CF and DE are joined as shown in figure. T...
Text Solution
|
- A cylinder rod of length 1, thermal conductivity K and area of cross s...
Text Solution
|
- The two ends of a rod of length L and a uniform cross-sectional area A...
Text Solution
|
- A rod of length L with sides fully insulated is made of a material who...
Text Solution
|
- A cylindrical rod of length l, thermal conductivity k and area of cros...
Text Solution
|
- One end of rod of length L and cross-sectional area A is kept in a fur...
Text Solution
|
- A rod of length l and cross-section area A has a variable thermal cond...
Text Solution
|
- Curved surface of a uniform rod is isolated from surrounding. Ends of ...
Text Solution
|