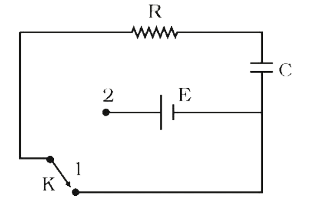
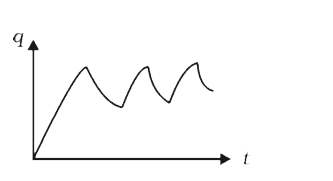
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- In the shown circuit involving a resistance Romega, capacitor of capac...
Text Solution
|
- In the circuit shown key is closed at t=0 with capacitor initially unc...
Text Solution
|
- The circuit involves two ideal cells connected to a 1 mu F capacitor v...
Text Solution
|
- A capacitor of capacitance C charged by battery at V volt and then dis...
Text Solution
|
- In the shown circuit involving a resistor of resistance R Omega , capa...
Text Solution
|
- In the shown circuit involving a resistor of resistance R Omega , capa...
Text Solution
|
- In the shown circuit involving a resistor of resistance R Omega , capa...
Text Solution
|
- Consider a simple RC circuit as shown in figure 1. Process 1 : In th...
Text Solution
|
- एक साधारण RC परिपथ को देखिए, जैसा चित्र 1 (Figure 1) में दर्शाया गया ह...
Text Solution
|