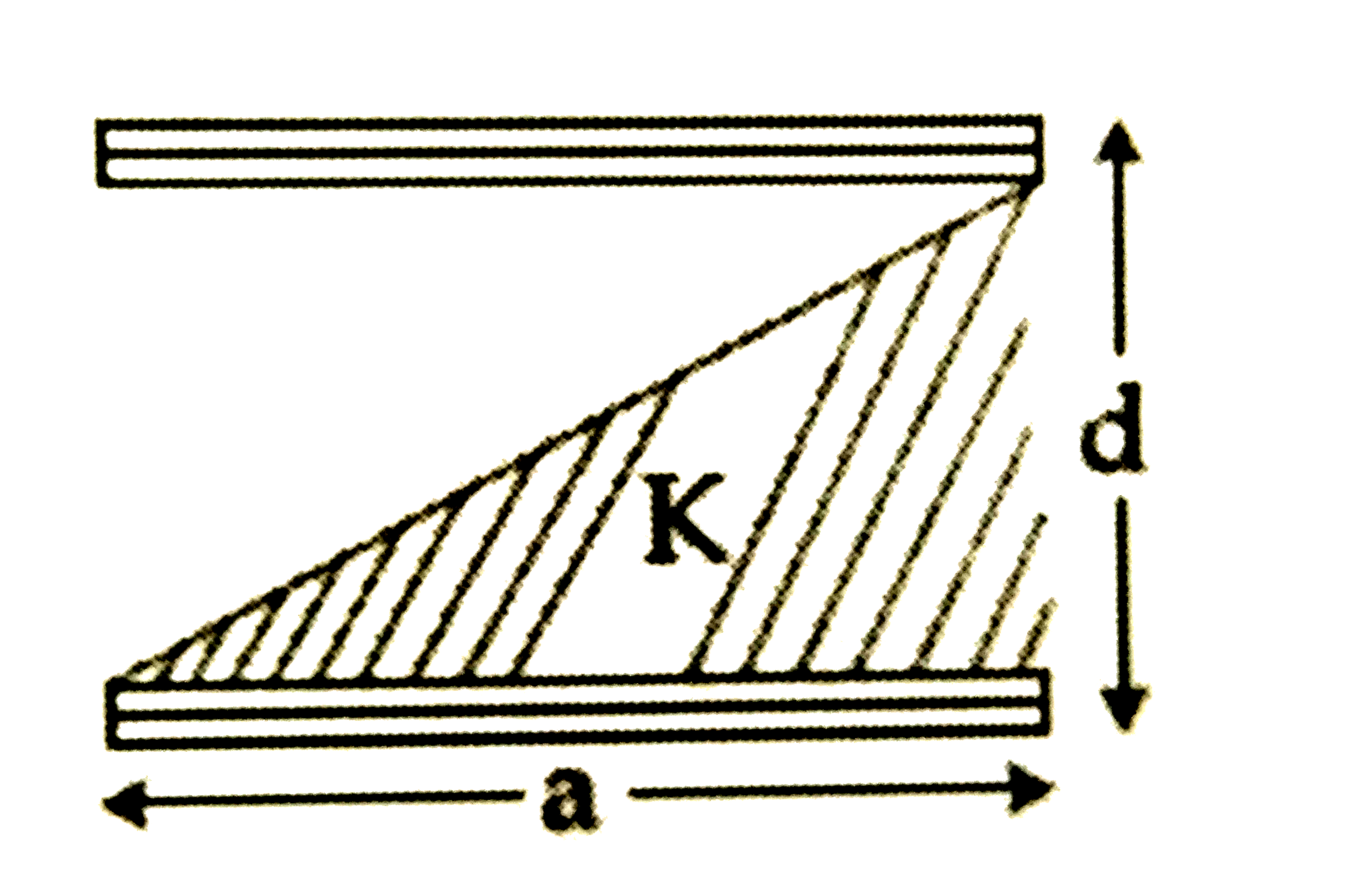
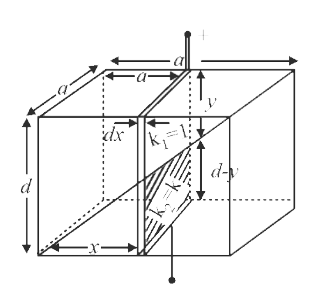
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- A paralled plate capacitor is made of two square plates of side 'a' , ...
Text Solution
|
- Figure shown a parallel-plate capacitor having square plates of edge ...
Text Solution
|
- A paralled plate capacitor is made of two square plates of side 'a' , ...
Text Solution
|
- The capacitor shown has square plates of side "L" and has gap d betwe...
Text Solution
|
- A parallel plate capacitor with air as the dielectric has capacitance ...
Text Solution
|
- Match the following Column - A and Column - B
Text Solution
|
- A parallel plate capacitor with air as the dielectric has capacitance ...
Text Solution
|
- A parallel plate capacitor, with plate separation d and plate area A, ...
Text Solution
|
- भुजा a वाली दो वर्गाकार प्लेटों को दूरी d पर रखकर एक समान्तर प्लेट संध...
Text Solution
|