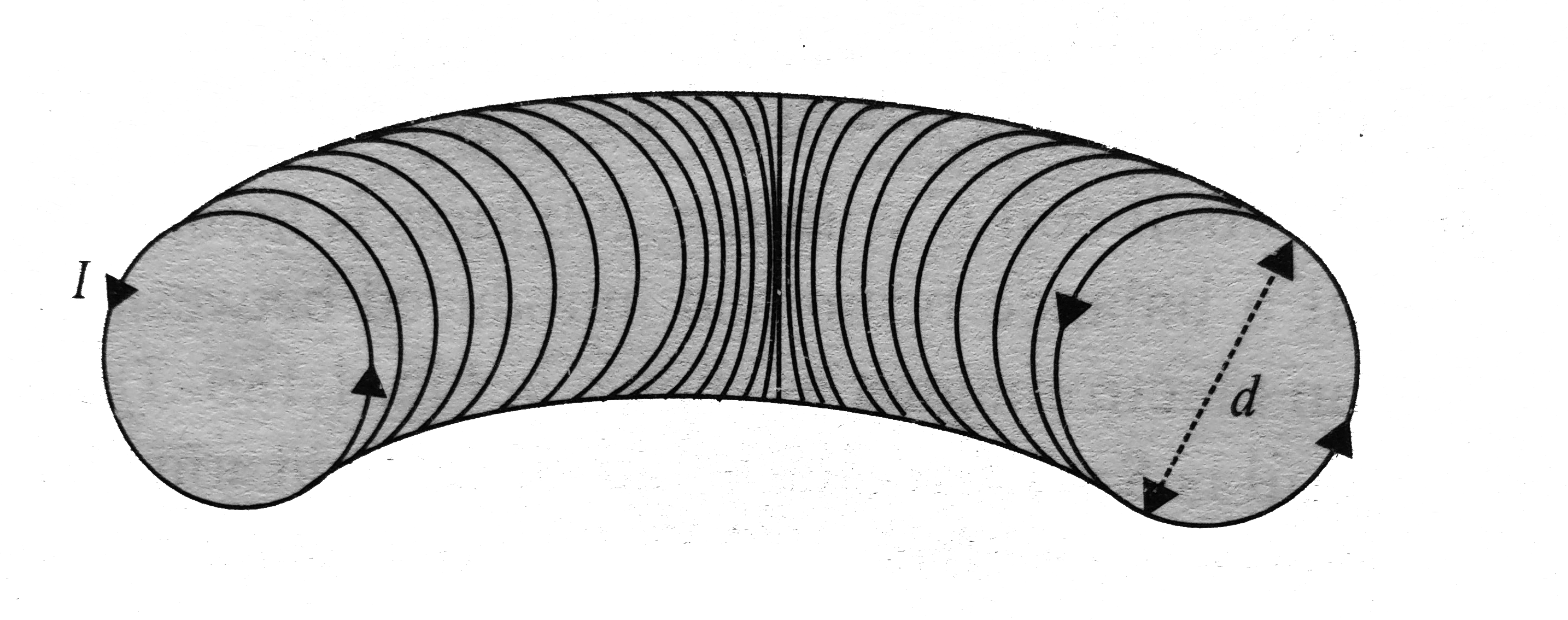
Text Solution
Verified by Experts
Recommended Questions
- Calculating the magnetic moment ( in Am^2) of a thin wire with a curre...
Text Solution
|
- Calculating the magnetic moment ( in Am^2 ) of a thin wire with a curr...
Text Solution
|
- A circular coil of N Turns and diameter d carries a current I. It is u...
Text Solution
|
- A toroid of total 1000 turns is made by using a tore of average radius...
Text Solution
|
- A closely wound solenoid of 750 turns and area of cross section of 5xx...
Text Solution
|
- Calculate the magnetic moment of a thin wire with a current I=0.8 A , ...
Text Solution
|
- A closlly wound coil of 1000 turns and cross sectional area 2xx10^(-4)...
Text Solution
|
- A circular coil of N turns and diameter d carries a current I . It is ...
Text Solution
|
- A circular coil of closely wound N turns and radius r carries a curren...
Text Solution
|