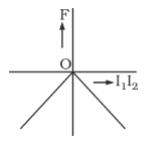
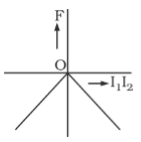
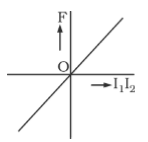
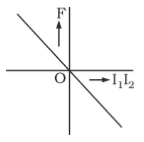
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Recommended Questions
- Two long straight parallel wires, carrying (adjustable) currents I(1...
Text Solution
|
- Two parallel infinite wires separated by distance d carry currents as ...
Text Solution
|
- Two parallel, long wires carry current i(1) and i(2) withi(1)gti(2). W...
Text Solution
|
- Two long parallel straight conductors carry current i(1) and i(2)(i(1)...
Text Solution
|
- Two parallel long wire carry currents i(1) and i(2) with i(1) gt i(2) ...
Text Solution
|
- Two long wire AB abd CD carry currents i(1) and i(2) in the direaction...
Text Solution
|
- Two parallel long wires carry currents i(1) and i(2) with i(1) gt i(2)...
Text Solution
|
- अनंत लंबाई के दो सीधे धारावाहिक तार एक-दूसरे से d दुरी पर परस्पर समांत...
Text Solution
|
- दो तार जिनमे I(1) और I(2) धारा प्रवाहित हो रही है एक दूसरे के समान्त...
Text Solution
|