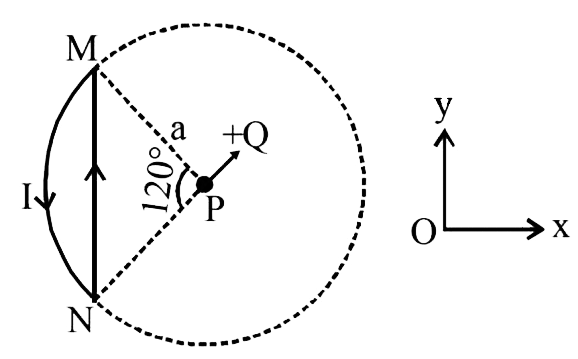
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- A wire loop carrying I is placed in the x-yplane as shown in fig. (...
Text Solution
|
- A conducting circular loop of radiius r carries a constant current i. ...
Text Solution
|
- A wire loop carrying I is placed in the x-y plane as shown in fig. (a)...
Text Solution
|
- A wire loop carrying a current I is placed in the xy-plane as shown in...
Text Solution
|
- A wire loop ABCDE carrying a current I is placed in the x-y plane as s...
Text Solution
|
- A wire loop carrying a current I is placed in the x-y plane. (a) If a ...
Text Solution
|
- What is the direction of the force acting on a charged particle q, mov...
Text Solution
|
- A conducting circular loop of radius r carries a constant current I. I...
Text Solution
|
- A wire loop carrying current I is placed in the x-y plane as shown in ...
Text Solution
|