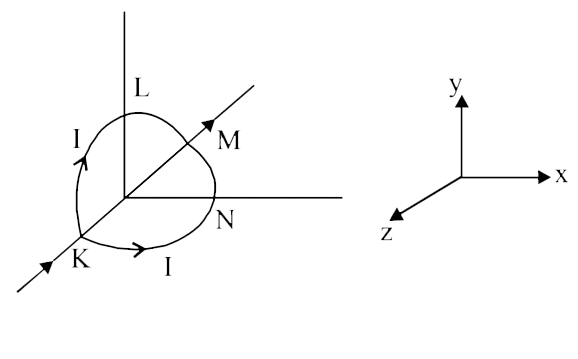
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- A circular loop of radius R is bent along a diameter and given a shap...
Text Solution
|
- A circular loop of radius R is bent along a diameter and given a shap...
Text Solution
|
- A circular loop of radius R is bent along a diameter and given a shape...
Text Solution
|
- A part of a long wire carrying a current i is bent into a circle of ra...
Text Solution
|
- A current carrying circular loop of radius R is placed in the x-y plan...
Text Solution
|
- Current I(0) is flowing through a bent wire atobtoctod in z-x plane as...
Text Solution
|
- An infinitely long straight conductor is bent into the shape as shown ...
Text Solution
|
- A circular loop of radius r, carrying a current I lines in y - z plane...
Text Solution
|
- A current carrying circular loop of radius R is placed in the x-y plan...
Text Solution
|