Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- A current of 10 A flows around a closed path in a circuit which is in ...
Text Solution
|
- A current of 10 A flows around a closed path in a circuit which is in ...
Text Solution
|
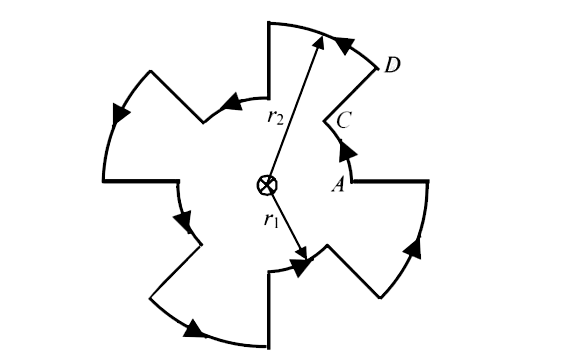
- A current path shaped as shown in figure produces a magnetic field at ...
Text Solution
|
- A current of 10 A flows around a closed path in a circuit which is int...
Text Solution
|
- A current I flows around a closed path in the horizontal plane of circ...
Text Solution
|
- निम्न चित्र में एक अपरिमित प्रतिरोधों वाला परिपथ प्रदर्शित है ...
Text Solution
|
- एक अर्द्धवृत्ताकार चाप की त्रिज्या 20 cm है और उसमे 10 A की धारा प्र...
Text Solution
|
- 10 ऐम्पियर की धारा, क्षैतिज तल में स्थित बन्द परिपथ में चित्रानुसार बह...
Text Solution
|
- चित्र में प्रदर्शित परिपथ का तुल्य प्रतिरोध ज्ञात कीजिए तथा R(3) व R(4...
Text Solution
|