Home
Class 12
CHEMISTRY
Assuming that water vapour is an ideal g...

Assuming that water vapour is an ideal gas, the internal energy change `(Delta U)` when `1 mol` of water is vapourised at `1` bar pressure and `100^(@)C`, (Given: Molar enthalpy of vapourization of water at `1` bar and `373K=41 kJ mol^(-1)` and `R=8.3J mol^(-1)K^(-1)`) will be:

A

`41.00 kJ mol^(-1)`

B

`4.100 kJmol^(-1)`

C

`3.7904 kJ mol^(-1)`

D

`37.904 kJmol^(-1)`

Text Solution

Verified by Experts

The correct Answer is:
D

`DeltaU = q+W = 41000 -1 xx 10^(5) xx (1 xx 8.314 xx 373)/(1 xx 10^(5)) -0 = (41000 - 3101.122) J = 37.9` kJ
Promotional Banner

Similar Questions

Explore conceptually related problems

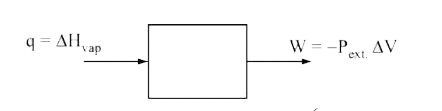
Assuming that water vapour is an ideal gas, the internal energy change (DeltaU) when 1 mole of water is vaporised at 1 ba r pressure and 100^(@)C, ( given : molar enthalpy of vaporization of water 41kJ mol^(-1) at 1 ba r and 373 K and R=8.3 J mol^(-1)K^(-1)) will be :

Assuming that water vapour is an ideal gas, the internal energy change (DeltaU) when 1 mole of water is vaporised at 1 bar pressure and 100^(@)C , (given: molar enthalpy of vaporisation of water -41KJmol^(-1) at 1 bar and 373K and R=8.3Jmol^(-1)Kmol^(-1) ) will be:

Assuming that water vapour is an ideal gas, the internal energy change (DeltaU) when 1 mol of water is vapourised at vapourisation of water at 1 bar and 373K=41 kJmol^-1 and R=8.3 Jmol^-1K^-1 will be

90 g of water spilled out from a vessel in the room on the floor. Assuming that water vapour behaving as an ideal gas, calculate the internal energy change when the spilled water undergoes complete evaporation at 100^(@)C . (Given the molar enthalpy of vaporisation of water at 1 bar and 373 K = 41 kJ mol^(-1) ).

Calculatte the molal elevation constant of water if molar enthalpy of vapourisation of water at 373K is 40.585 kJ mol^(-1) .