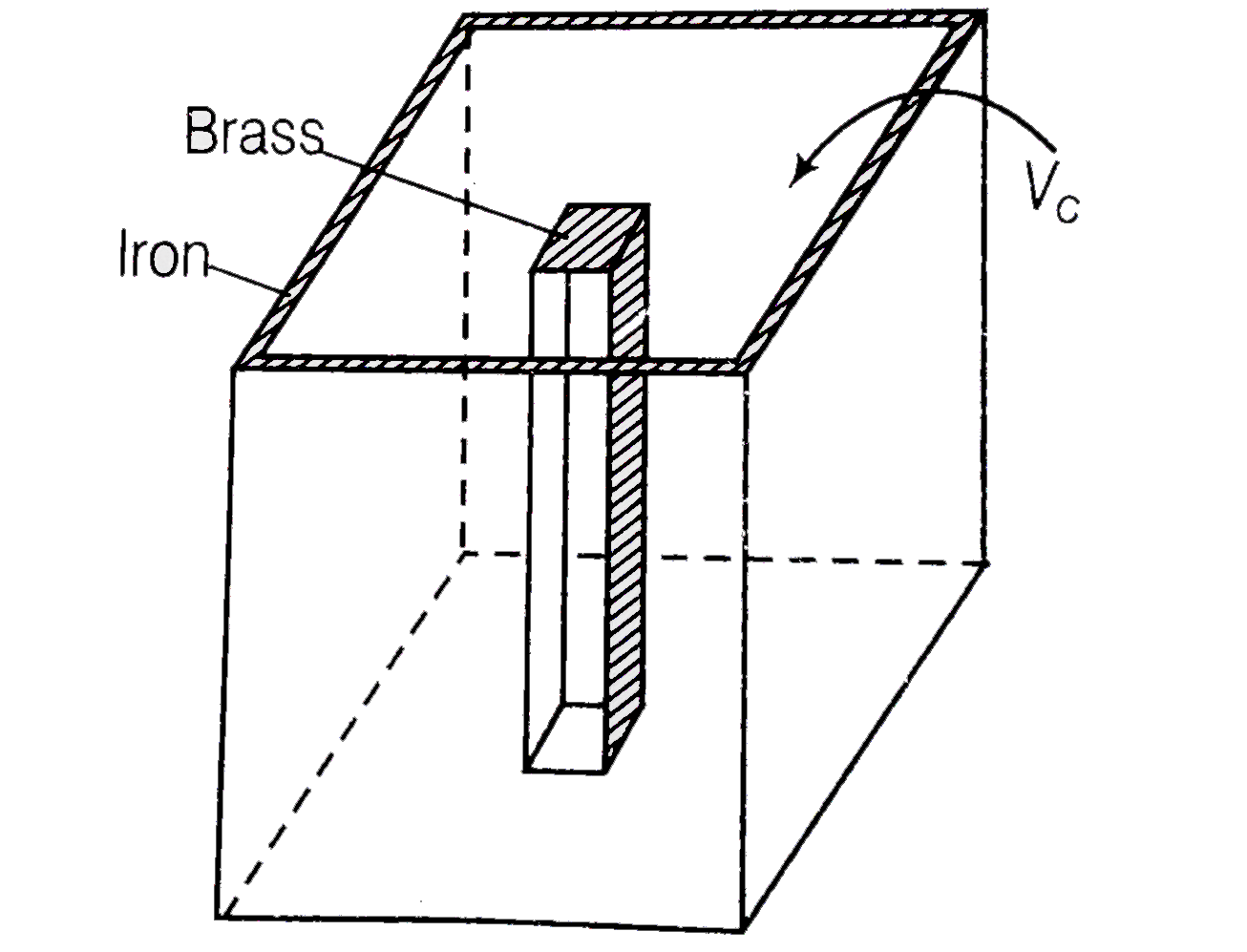Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR-THERMAL PROPERTIES OF MATTER-Very short Answer type Questions
- Is the bulb of a thermoeter made of diathermic or adiabatic wall ?
Text Solution
|
- A student records the initial length l, change in temperature Delta T ...
Text Solution
|
- Why does a metal bar appear hotter than a wooden bar at the same tempe...
Text Solution
|
- Calculate the temperature which has same number value on Celsius and F...
Text Solution
|
- These days people use steel utensiles with copper bottom. This is supp...
Text Solution
|
- find out the increase in moment of inertia I of a uniform rod (coeffic...
Text Solution
|
- During summers in india, one of the common practice to keep cool is to...
Text Solution
|
- 100 g of water is supercooled to - 10^@C. At this point, due to same d...
Text Solution
|
- One day in the morning, Ramesh filled up 1//3 bucket of hot water fro...
Text Solution
|
- We would like to perpare a scale whose length does not change with tem...
Text Solution
|
- We would like to make a vessel whose volume does not change with temp...
Text Solution
|
- Calculate the stress developed inside a tooth cavity filled with coppe...
Text Solution
|
- A rail track made of steel having length 10 m is clamped on a railway ...
Text Solution
|
- A thin rod, length L(0) at 0^(@)C and coefficient of linear expansion ...
Text Solution
|
- Ac cording to Stefan' law of radiation, a black body radiates energy s...
Text Solution
|