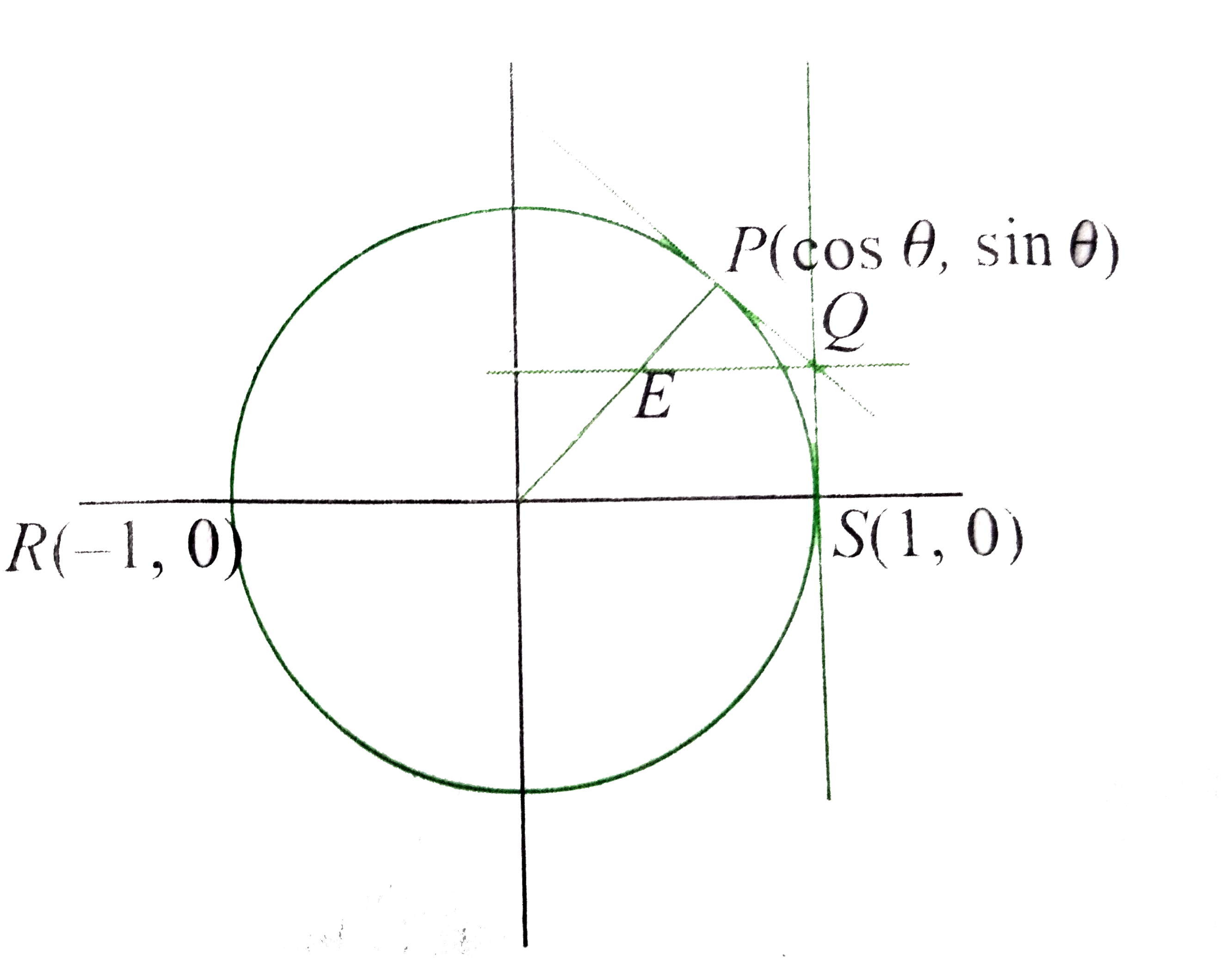
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The tangent at any point to the circle x^2+y^2=r^2 meets the coordinat...
Text Solution
|
- The tangent at any point P on the circle x^2+y^2=4 meets the coordinat...
Text Solution
|
- Find the locus of point P such that the tangents drawn from it to the ...
Text Solution
|
- The tangent at P, any point on the circle x^(2)+y^(2)=4, meets the coo...
Text Solution
|
- A line lx+my+n=0 meets the circle x^(2)+y^(2)=a^(2) at points P and Q....
Text Solution
|
- A variable plane at constant distance p form the origin meets the coor...
Text Solution
|
- A tangent to the circle x^(2)+y^(2)=4 meets the coordinate axes at P a...
Text Solution
|
- A line through the origin meets the circle x^(2) +y^(2) =a^(2) at P ...
Text Solution
|
- एक रेखा lx + my+n= 0, वृत्त x^2 + y^2 =a^2 के बिन्दु P व Q पर मिलती ह...
Text Solution
|