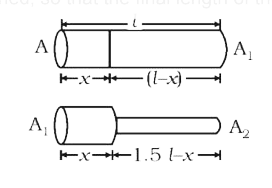
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- In order to increase the resistance of a given wire of uniform cross s...
Text Solution
|
- In order to increase the resistance of a given wire of unknown of unif...
Text Solution
|
- Consider a wire of length l, area of cross section A, and resistivity ...
Text Solution
|
- A copper wire of resistance R(0) is strerched till its length is incre...
Text Solution
|
- In order to quadruple the resistance of a uniform wire, a part of its ...
Text Solution
|
- If a wire is stretched to four times its length, then the specific res...
Text Solution
|
- If a wire of resistance 25Omega is uniformly stretched until its lengt...
Text Solution
|
- A wire of resistance 12Omega is stretched uniformly till its length be...
Text Solution
|
- यदि किसी तार को खींचकर उसकी लंबाई चार गुनी कर दी जाय, तो उसका विशिष्ट ...
Text Solution
|