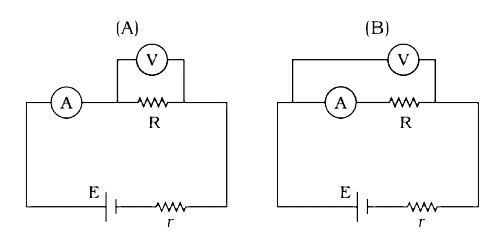
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Resistance value of an unknown resistor is calculated using the formul...
Text Solution
|
- The value of resistance of an unknown resistor is calculated using the...
Text Solution
|
- The value of resistance of an unknown resistor is calculated using the...
Text Solution
|
- The ammeter A reads 2A and the voltmeter V reads 20V, the value of res...
Text Solution
|
- For the adjoining circuit diagram, the readings of ammeter and voltmet...
Text Solution
|
- In the adjoining circuit diagram, the readings of ammeter and voltmete...
Text Solution
|
- In the circuit shown below, the ammeter and the voltmeter readings are...
Text Solution
|
- एक धारामापी का प्रतिरोध Rg अमीटर का प्रतिरोध RA तथा वोल्टमीटर का प्रति...
Text Solution
|
- Resistance value of an unknown resistor is calculated using the formul...
Text Solution
|