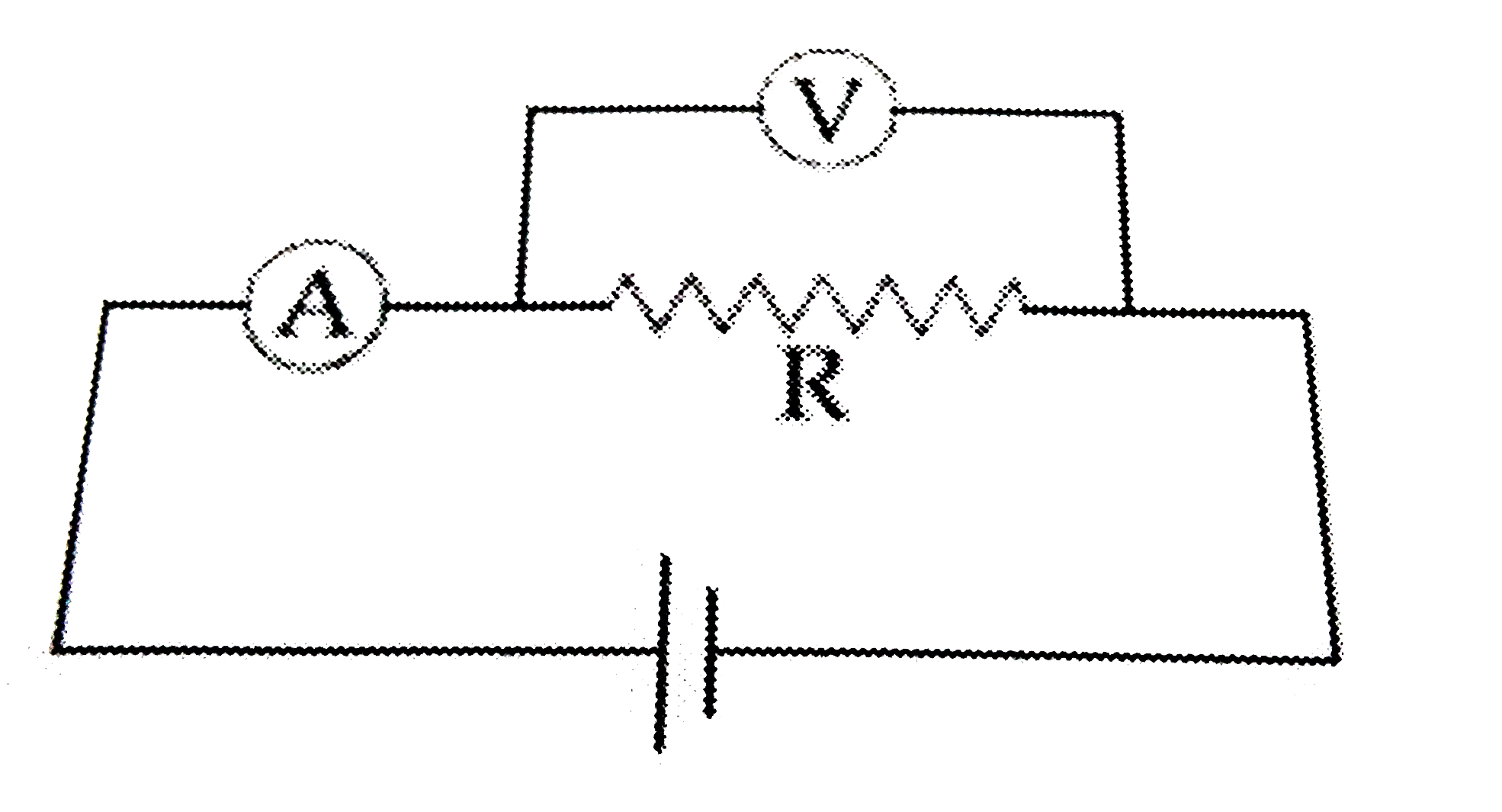
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The actual value of resistance R, shown in the figure is 30 Omega. Thi...
Text Solution
|
- Determine the resistance r if an ammeter shows a current of I = 5 A an...
Text Solution
|
- The value of resistance of an unknown resistor is calculated using the...
Text Solution
|
- In the, Ohm's law experiment ot find resistance of unknown resistor R,...
Text Solution
|
- A voltmeter of resistance R(V) and an ammeter of resistance R(A) are c...
Text Solution
|
- The circuit shown here is used to measure resitance R. An ammeter show...
Text Solution
|
- An ammeter A, a voltmeter V and a resistance R are connected as shown ...
Text Solution
|
- For the adjoining circuit diagram, the readings of ammeter and voltmet...
Text Solution
|
- The actual value of resistance R, shown in the figure is 30 Omega . Th...
Text Solution
|